[경고] 아래 글을 읽지 않고 "포물선의 방정식"을 보면 바보로 느껴질 수 있습니다.
포물선(抛物線, parabola)은 물건을 하늘로 던질 때 중력(gravity)과 속도(velocity)가 만드는 물체의 궤적이다. [그림 1]은 분수가 물을 하늘로 쏠 때 나타나는 포물선 형태를 보여준다.
[그림 1] 분수가 만드는 포물선(출처: wikipedia.org)
[그림 2] 포물선의 기하학적 정의(출처: wikipedia.org)
포물선은 기하학적으로 [그림 2]처럼 정의한다. 초점(focus) $\bar F$ = $(0, f)$에서 점 $\bar P_i$ = $(x_i, y_i)$까지 거리가 점 $\bar P_i$에서 준선(準線, directrix) $L$[$y$ = $-f$]까지 거리와 같은 점을 모두 모으면 포물선이 된다. 준선은 2차 곡선을 정의하거나 생성할 때 쓰이는 기준선이다. 이를 방정식으로 표현하면 다음과 같다.
(1)
여기서 $(x, y)$는 포물선 위의 점이며 $f$[= $1/(4a)$]는 포물선의 초점이다.
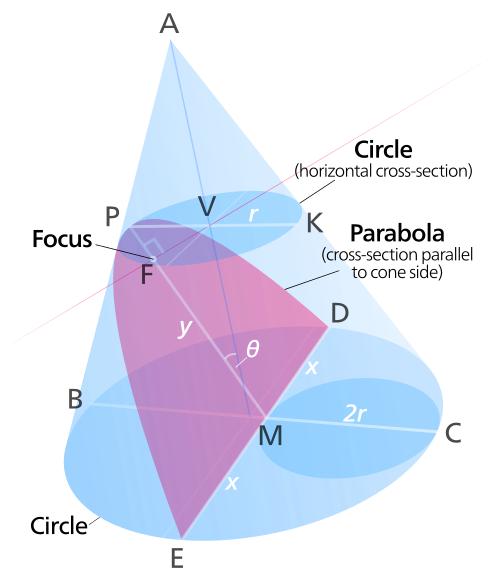
[그림 3] 원뿔로 만드는 포물선(출처: wikipedia.org)
[그림 3]에 소개한 초보적인 기하학을 이용해 포물선을 정의할 수 있다. 이 방법은 아폴로니우스Apollonius of Perga(대략 기원전 240–190)에 의해 제안되었다. 먼저 [그림 3]에서 원뿔(cone)의 꼭지점을 $A$라 한다. 다음에 원뿔을 잘라 두 개의 원[짙은 파란색]을 만든다. 첫번째 원은 선분 $\overline{PK}$를 지름($2r$)으로 가진다. 두번째 원은 선분 $\overline{BC}$가 지름이다. 원뿔 바깥선과 평행하게 선분 $\overline{PM}$ = $y$을 그어 선분 $\overline{MC}$ = $2r$이 되게 한다. 선분 $\overline{PM}$은 원뿔 바깥선과 평행이므로 $\angle PBM$ = $\angle PMB$가 성립하여 $\triangle PBM$은 이등변 삼각형이 된다. 선분 $\overline{PM}$이 원뿔 기준선[점 $A$에서 두번째 원에 내린 수직선]과 이루는 각도를 $\theta$라 하면 $\overline{BM}$ = $2 y \sin \theta$가 된다. 또한 선분 $\overline{DE}$ = $2x$는 반지름이 $r$인 원에 접하므로 이 원에 수직이며, 탈레스의 정리(Thales' theorem)에 의해 $\angle BEC$도 수직이다. 따라서 다음이 성립한다.
(2)
식 (1)을 고려하면 포물선의 초점은 $f$ = $r \sin \theta$가 된다.
[그림 4] 새로운 준선을 가진 포물선(출처: wikipedia.org)
관점을 좀 바꾸어보면 [그림 2]의 준선은 [그림 4]처럼 바꿀 수 있다. [그림 4]의 준선 $M$은 초점 $\bar F$ = $(0, f)$의 아래가 아닌 초점 위에 있다. 예를 들어, 준선 $M$이 $y$ = $g$[$g > 0$]에 있다고 가정한다. 그러면 [그림 2]와 [그림 4]에 있는 준선 $L$과 $M$ 간의 거리는 항상 $\overline{Q_i P_i} + \overline{P_i R_i}$ = $|g - (-f)|$ = $|f + g|$가 된다. [그림 2]의 결과에 의해 $\overline{Q_i P_i}$ = $\overline{F P_i}$이기도 하다. 따라서 [그림 4]의 경우에도 초점에서 준선까지 가는 거리는 항상 일정하므로, 식 (1)과 같은 포물선의 방정식을 다음처럼 얻을 수도 있다.
(3)
여기서 $f > 0$, $y < g$이다. 준선이 양의 $y$축에 있더라도 포물선의 방정식은 식 (1)과 동일하게 얻어진다. 또한 $g$가 0보다 크기만 하면, $g$에 관계없이 초점과 준선 사이의 거리는 항상 동일하다. 별것 아닌 [그림 4]의 개념이 현존하는 반사판 안테나(reflector antenna) 혹은 조명 기구의 기본적인 원리이다.
[그림 5] 포물형 반사판 안테나(출처: wikimedia.org)
[그림 6] 태양열 조리기(출처: wikipedia.org)
.jpg/640px-Headlight_(2966062110).jpg)
[그림 7] 자동차의 전조등(출처: wikipedia.org)
[그림 5–7]은 포물선의 원리를 적용한 여러 제품을 보여준다. [그림 5]는 포물형 반사판 안테나(parabolic reflector antenna)이다. 급전부(feed)는 포물선의 초점에 있다. 급전부에서 나온 전자파는 포물형 금속 반사판에서 반사되어 준선 방향에 수직인 방향으로 전달된다. 이게 고이득 안테나를 만드는 일반 원리가 된다. [그림 6]은 태양열 조리기(solar cooker)의 예를 보여준다. 태양빛이 포물형 거울 반사판에서 반사되어 초점에 집속된다. 초점에 조리기를 두면 태양열이 강하게 집속되어 요리가 가능하다. [그림 7]은 자동차의 전조등(headlight)이다. 초점 위치에 광원을 두고 포물형 거울 반사판에 쏘면 대부분의 빛이 전방으로 강하게 전달된다.
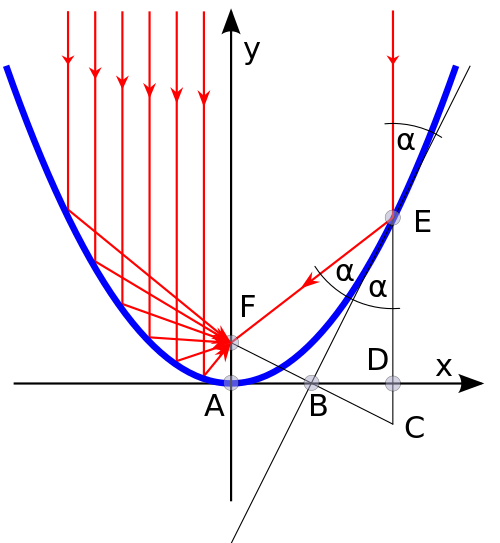
[그림 8] 포물선의 반사 원리(출처: wikipedia.org)
그러면 [그림 5–7]의 동작 원리를 간단한 포물선 개념으로 설명한다. 이를 위해 [그림 8]에 제시한 포물면의 반사 특성을 계산해야 한다. 준선에 수직인 방향으로 광선(ray)이 들어온다고 생각한다. 이 광선과 포물면이 이루는 각도는 $\alpha$이다. 또한 [그림 2]와 같이 음의 $y$축에 있는 준선 위의 점을 $C$라 한다. 그러면 포물선의 정의에 의해 삼각형 $\triangle ECF$는 이등변 삼각형이다.[∵ 초점에서 포물선 점 $(x, y)$의 거리와 포물선 점 $(x, y)$과 준선까지 거리는 항상 같다.] 선분 $\overline{CF}$와 $\overline{EB}$가 수직임을 증명하기 위해 식 (1)에 있는 포물선의 방정식을 이용한다.
(4)
(4)
여기서 $\bar T$는 접선의 기울기이다. 삼각형 $\triangle ECF$는 이등변 삼각형이면서 선분 $\overline{EB}$는 선분 $\overline{CF}$에 수직하므로 $\angle FEB$ = $\angle CEB$가 된다. 즉, 준선에 수직인 방향으로 들어온 광선은 입사각과 동일한 각도로 반사되어 초점으로 들어간다. 이런 성질은 빛에 대한 금속면 반사 법칙과 동일하다. 그래서, 포물형 반사판에 반사된 빛은 초점에 모두 모인다.
[그림 9] 유한한 포물선의 모양
포물선이 복잡하기는 하지만 [그림 9]의 $D, d$를 알면 쉽게 포물선 상수 $a$ 혹은 초점 $f$를 결정할 수 있다.
(5)
식 (5)는 지름 $D$, 깊이 $d$를 가진 유한한 포물선을 측정하여 포물선 상수 $a$와 초점 $f$를 결정하기 위한 가장 쉬운 방법이다. 예를 들어 [그림 9]와 같은 포물선은 다음 식처럼 표현된다.
(6)
식 (6)으로부터 $x$ = $D/2$이면 당연히 $y$ = $d$가 나온다. 만약 포물선이 놓여있는 지름 위치[$x$의 범위 = $(-D/2, D/2)$]가 $y$ = $0$이 된다면 포물선의 방정식은 다음처럼 바뀐다.
(7)
식 (7)에서 $x$ = $\pm D/2$이면 $y$ = $0$이 된다.
포물선의 표현에 사용한 식 (1)은 2차 곡선을 정의하거나 분류할 때 사용하는 이심률(離心率, eccentricity)의 정의이다. 식 (1)과 동일하게, 초점 $\bar F$에서 2차 곡선 위의 점 $\bar P$까지 거리와 준선(準線, directrix)에서 $\bar P$까지 거리의 비율을 이용해 이심률을 다음처럼 정의한다.
(8)
[그림 10]처럼 포물선이 회전한 경우는 포물선의 방정식이 식 (1)처럼 간단히 표현되지 않는다. [그림 10]의 기하 구조에 대해, 식 (1)과 같은 논리로 거리를 계산한다.
포물선의 표현에 사용한 식 (1)은 2차 곡선을 정의하거나 분류할 때 사용하는 이심률(離心率, eccentricity)의 정의이다. 식 (1)과 동일하게, 초점 $\bar F$에서 2차 곡선 위의 점 $\bar P$까지 거리와 준선(準線, directrix)에서 $\bar P$까지 거리의 비율을 이용해 이심률을 다음처럼 정의한다.
(8)
여기서 $L$은 준선에서 $\bar P$까지 거리이다. 식 (8)에 의해 포물선의 이심률은 1이다.
[그림 10] 회전한 포물선(출처: wikipedia.org)
(9)여기서 포물선 위의 점은 $(x, y)$, 초점은 $\bar F$ = $(f_x, f_y)$, 준선은 $ax+by+c$ = $0$, 준선과 포물선의 거리는 점과 직선 사이의 거리를 사용, 나머지 항을 담아놓은 함수는 직선처럼 $F(x, y)$ = $Ax + By + C$로 선택한다. 식 (9)에서 유추하여 포물선이 될 수 있는 임의의 2차 곡선은 다음 형태를 가진다.
(10)여기서 $D$는 원뿔 곡선의 판별식(discriminant of conic section)이다. 신기하게도 원뿔 곡선의 판별식은 2차 방정식의 판별식과 부호만 다르고 완전 동일하다. 만약 판별식이 $D$ = $0$으로 나오면, 이 2차 곡선은 [그림 10]과 같은 회전한 포물선이 된다.
(5)
(6)
(7)
(8)
(9)
(10)
(11)
(13)
(14)
(35)