1. 멱급수 기반 상미분 방정식 해법
2. 스튀름–리우빌 이론

[그림 1] 르장드르 다항식이 출현하는 물체의 질량 분포와 중력(출처: wikipedia.org)
식 (1)에 있는 르장드르의 미분 방정식(Legendre's differential equation)은 다소 복잡한 모양을 가지고 있다.
 (1a)
(1a) (1b)
(1b)
식 (1)에서 $x = \cos\theta$로 치환하면 조금은 단순해진 미분 방정식(differential equation)을 얻을 수 있다.
 (2)
(2) (3)
(3)식 (2)를 식 (1)에 대입해서 정리하고 $1 - x^2$ = $\sin^2 \theta$ 및 $\frac{d}{d\theta}(\sin \theta \frac{dy}{d\theta})$ = $\cos \theta \frac{dy}{d\theta} + \sin \theta \frac{d^2 y}{d\theta^2}$를 이용하면, 식 (3)이 자연스럽게 유도된다. 식 (1), (3)에서 $m$ = $0$인 경우는 미분 방정식을 더욱 간략화할 수 있다.
 (4a)
(4a) (4b)
(4b) (5)
(5)
식 (1)보다는 간편한 식 (4)의 해를 구한다. 점 $x$ = $0$은 미분 방정식 (4)의 정상점(ordinary point)이라서 다음과 같은 단순한 멱급수(power series) 전개가 가능하다.
 (6)
(6)
식 (6)을 식 (4)에 전개해 항별로 정리하면 다음을 얻는다.
 (7)
(7)
식 (7)이 $x$에 관계없이 $0$이기 위해서는 각 항이 모두 $0$이어야 한다. 따라서 르장드르 미분 방정식을 위한 다음 재귀 관계(recurrence relation)를 얻을 수 있다.
 (8)
(8)
식 (8)의 분자를 인수 분해하면 다음과 같다.
 (9)
(9)
식 (9)를 이용해 멱급수 해를 구하려면 $a_0, a_1$을 정해야 한다. 먼저 $a_0$ = $1$, $a_1$ = $0$이라 정하면 미분 방정식의 해는 다음처럼 표현되어야 한다.
 (10a)
(10a) (10b)
(10b)
반대로 $a_0$ = $0$, $a_1$ = $1$라 정하면 해는 다음처럼 다르게 표현된다.
 (11a)
(11a) (11b)
(11b) 식 (10)과 (11)을 이용하여 $m$ = $0$인 르장드르 미분 방정식의 일반해(general solution)는 다음처럼 쓸 수 있다.
 (12)
(12)
특별히 차수(次數, degree) $n$이 정수인 경우는 르장드르 미분 방정식의 해가 무한 급수(infinite series)가 아니고 다항식(polynomial expression)이 될 수 있다. 차수 $n$이 짝수인 경우는 식 (10)이 다항식으로 표현되며, 차수 $n$이 홀수인 경우는 식 (11)이 다항식으로 된다. 이 경우의 해는 르장드르 다항식(Legendre polynomials) $P_n(x)$라 부른다[2]. 식 (10)과 (11)을 이용해 각 차수에 대한 르장드르 다항식을 써보면, 모든 차수 $n$에 대해 식 (13) 혹은 [표 1]처럼 유한 급수(finite series)로 표현할 수 있다.
 (13)
(13)[그림 1]처럼 원점에서 벗어나 질량이 자유롭게 분포하는 물체의 중력 포텐셜(gravitational potential)을 구할 때는 르장드르 다항식이 꼭 필요하다.
 (14)
(14)
 (15)
(15)
 (16)
(16)
 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
 (23)
(23)
 (24)
(24)
 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
 (29)
(29)
[표 1] 르장드르 다항식의 유한 급수 표현식, $P_n(x)$
| 차수(degree), $n$ | $P_n(x)$ |
|---|---|
| 0 | $1$ |
| 1 | $x$ |
| 2 | $\displaystyle{\frac{1}{2}}(3x^2-1)$ |
| 3 | $\displaystyle{\frac{1}{2}}(5x^3-3x)$ |
| 4 | $\displaystyle{\frac{1}{8}}(35x^{4}-30x^{2}+3)$ |
| 5 | $\displaystyle{\frac{1}{8}}(63x^{5}-70x^{3}+15x)$ |
| 6 | $\displaystyle{\frac{1}{16}}(231x^{6}-315x^{4}+105x^{2}-5)$ |
| 7 | $\displaystyle{\frac{1}{16}}(429x^{7}-693x^{5}+315x^{3}-35x)$ |
| 8 | $\displaystyle{\frac{1}{128}}(6435x^{8}-12012x^{6}+6930x^{4}-1260x^{2}+35)$ |
| 9 | $\displaystyle{\frac{1}{128}}(12155x^{9}-25740x^{7}+18018x^{5}-4620x^{3}+315x)$ |
| 10 | $\displaystyle{\frac{1}{256}}(46189x^{10}-109395x^{8}+90090x^{6}-30030x^{4}+3465x^{2}-63)$ |
| 11 | $\displaystyle{\frac{1}{256}}(88179 x^{11} - 230945 x^9 + 218790 x^7 - 90090 x^5 + 15015 x^3 - 693 x)$ |
식 (13)에서 르장드르 다항식은 다음 성질을 만족하기 위해 식 (10)과 (11)의 상수를 조정하였다.
 (14)
(14)
르장드르 다항식과는 다른 제2해(the second solution)에 해당하는 식은 다항식이 아니고 무한 급수이다. 이 무한 급수도 식 (10)과 (11)을 이용해 구한다. 예를 들어, $n$ = $0$인 경우는 식 (10)이 다항식을 만들고 식 (11)은 다음과 같은 무한 급수를 만든다.
 (15)
(15)
식 (15)는 스튀름–리우빌 이론(Sturm–Liouville theory)으로 구할 수도 있다. 이 이론에 의해 제2해는 다음처럼 주어진다.
 (16)
(16)
여기서 $\psi_1$은 미리 알고 있는 제1해(the first solution)이며 $\psi_2$는 제2해이다. $\psi_1$ = $P_0(x)$ = $1$을 식 (16)에 대입해 적분한다.
 (17)
(17)
르장드르 다항식 $P_n(x)$와는 다른 제2해는 무한 급수이며 보통 $Q_n(x)$로 표현한다. 해 $P_n(x)$는 $n$차 다항식이며 $Q_n(x)$는 다항식이 아닌 근본 이유는 직교 다항식(orthogonal polynomial)에 있다. 식 (1)처럼 직교 다항식을 생성하는 미분 방정식의 해는 하나만 다항식이며, 나머지 해는 스튀름–리우빌 이론(Sturm–Liouville theory)에 의해 다항식일 수 없다. 비슷한 방법으로 $n$ = $1$을 구하면 다음과 같다.
 (18)
(18)
식 (18)에서 상수 $a$는 별 의미없다. 정적분에서 시작점 $a$를 대입하면 원시 함수값은 결국 상수가 되므로, $Q_n(x)$를 표현할 때 과감하게 삭제할 수 있다.[$\because$ $a$와 관련된 적분 상수($c$)가 있더라도 결국 $cP_n(x)$가 되므로, 독립적인 제2해 $Q_n(x)$가 아닌 제1해 $P_n(x)$에 속한다.] 차수 $n \ge 2$인 경우는 르장드르 미분 방정식의 재귀 관계(recurrence relation)를 이용해 구한다. $P_n(x)$와 $Q_n(x)$는 식 (4)의 르장드르 미분 방정식을 만족하므로 이 둘을 통칭하여 르장드르 함수(Legendre function)라 한다. 더 자세하게 보면 $P_n(x)$는 제1종 르장드르 함수(Legendre function of the first kind)이며 $Q_n(x)$는 제2종 르장드르 함수(Legendre function of the second kind)이다.
식 (10)이나 (11)과 같은 무한 급수(infinite series)를 다룰 때 조심해야 할 부분은 수렴 특성이다. 르장드르 함수는 식 (9)와 같은 깔끔한 재귀 관계가 있어 수렴성 해석은 매우 쉽다. 수열 $a_k$에서 $k+2$번째 항과 $k$번째 항의 비율을 다음처럼 계산한다.
 (19)
(19)
첨수(index) $k$가 무한대로 갈 때 위와 같은 특성이 있다. 무한 등비 급수(infinite geometric series)와 식 (19)를 비교하면 르장드르 함수가 수렴하는 구간은 $|x| < 1$임을 알 수 있다. 물론 $n$이 정수인 경우는 식 (13)과 같은 르장드르 다항식을 만들 수 있기 때문에 수렴 구간은 무한대이다.
이상의 성질을 이용하면 $m \ne 0$ 경우인 식 (1)의 해를 구할 수 있다. 이를 위해 다음과 같은 변수 치환을 한다.
 (20)
(20)
식 (20)을 식 (1)에 대입해 정리하면 $u$에 대한 미분 방정식을 얻는다.
 (21)
(21)만약 $m$ = $0$이면, 식 (21)은 식 (4)가 된다. 미분 방정식 (21)의 의미를 알기 위해 식 (21)을 $x$에 대해 미분한다.
 (22)
(22)
신기하게도 한 번 미분하면 $m$이 1만큼 커진다. 이 성질에 의해 두 번 미분하면 $m$이 2만큼 커진다. 이 특성을 거꾸로 유추하면 식 (21)은 식 (4)를 $m$번 미분한 식이다. 따라서 식 (1)의 해는 다음처럼 쓸 수 있으며 버금 르장드르 함수(associated Legendre function)라 명한다.
 (23)
(23)
여기서 $P_n^m(x)$는 제1종 버금 르장드르 함수(associated Legendre function of the first kind)이며 $Q_n^m(x)$는 제2종 버금 르장드르 함수(associated Legendre function of the second kind)이다. 식 (23)에 나오는 첨자 $n, m$은 각각 차수(次數, degree)와 계수(階數, order) 혹은 계층수(階層數)라 부른다. 여기서 계수는 미지수와 곱셈으로 연계되는 계수(係數, coefficient)와 한자가 완전 다르며 구별을 위해 계층수라고 명확히 부를 수도 있다.
[표 2] 버금 르장드르 함수의 유한 급수 표현식, $P_n^m(x)$
| 계층수(order), $m$ | 차수(degree), $n$ | $P_n^m(x)$ |
|---|---|---|
| 1 | 1 | $-\sqrt{1-x^2}$ |
| 1 | 2 | $-3x\sqrt{1-x^2}$ |
| 2 | 2 | $3(1-x^2)$ |
| 1 | 3 | $\displaystyle{\frac{3}{2}}(1-5x^2)\sqrt{1-x^2}$ |
| 2 | 3 | $15x(1-x^2)$ |
| 3 | 3 | $-15\sqrt{(1-x^2)^3}$ |
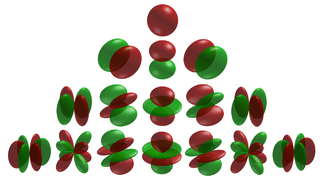
[그림 2] 구면 조화 함수의 모양(출처: wikipedia.org)
식 (23)의 상수 $(-1)^m$은 없어도 되지만 버금 르장드르 함수를 이용해 정의하는 구면 조화 함수(球面 調和函數, spherical harmonics) 수식을 간편하게 만들기 위해 도입한 양이다. 상수 $(-1)^m$의 정식명은 콘던–쇼틀리 위상(Condon–Shortley phase)이다. 콘던–쇼틀리 위상을 생략한 경우는 다음처럼 버금 르장드르 함수를 표시한다.
 (24)
(24)
식 (23)의 정의로 인해 $n, m$이 정수인 제1종 버금 르장드르 함수 $P_n^m(x)$는 다음 관계가 반드시 성립한다.
 (25)
(25)
식 (26)에 제시한 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)을 이용하면, 식 (4)를 다음과 같은 스튀름–리우빌 형태(Sturm–Liouville form)로 쓸 수 있다.
 (26)
(26) (27)
(27)
따라서 르장드르 미분 방정식은 $p(x)$ = $1 - x^2$, $q(x)$ = $0$, $r(x)$ = $1$, $\lambda$ = $n(n+1)$인 스튀름–리우빌 미분 방정식이 된다. 식 (1)에 있는 다소 복잡한 르장드르 미분 방정식은 $p(x)$ = $1 - x^2$, $q(x)$ = $m^2/(1 - x^2)$, $r(x)$ = $1$, $\lambda$ = $n(n+1)$인 스튀름–리우빌 미분 방정식으로 간주한다. 왜냐하면 $x$ = $\pm 1$에서 발생하는 특이점을 처리하기 위해, 스튀름–리우빌 이론에서 특별한 제약이 없는 $q(x)$에 특이점이 있는 함수를 배정하기 때문이다. 어떤 경우에는 $p(x)$ = $1 - x^2$, $q(x)$ = $-n(n+1)$, $r(x)$ = $1/(1-x^2)$, $\lambda$ = $-m^2$라고 설정해서, $r(x)$가 $x$ = $\pm 1$에서 발산하도록 내버려둔다. 다만 $r(x)$는 발산하더라도 고유 함수 $\psi_m(x)$의 적분 $\int_{-1}^1 [\psi_m(x)]^2 r(x) \, dx$는 존재하도록 고유값 $\lambda$를 선택한다.
식 (1)로 표현한 미분 방정식에서 고유값 $\lambda$는 항상 $n(n+1)$이어야 할까? 아니다. 고유값은 경계 조건만 만족하면 어떤 값이든 가능하다. 하지만 르장드르 함수가 정의된 $[-1, 1]$에서 함수값을 유한하게 만들려면, 최소한 $\lambda$ = $n(n+1)$이 되어야 한다. 이 특성을 염두에 두고 식 (8)을 고유값 $\lambda$로 다시 쓴다.
 (28)
(28)지표(index) $k$가 매우 커질 때에 $a_{k+2} / a_k$는 1에 수렴해서, $x$ = $\pm 1$에서 $P_n(x)$는 발산하거나 정의되지 않는다.
 (29)
(29)점 $x$ = $\pm 1$의 발산 현상을 잡는 유일한 방법은 $\lambda$ = $n(n+1)$로 놓고 특정한 $k$에서 $k$ = $n$이 되어 $a_{k+2}$ = $0$이 되는 방식 뿐이다. 다만 $\lambda$ = $n(n+1)$인 조건을 잡더라도 $k$는 2칸씩 커지므로, $k$ = $n$이 될 수 없는 경우가 생긴다. 이때는 식 (15)처럼 $x$ = $\pm 1$에서 발산하는 $Q_n(x)$가 된다. 대신 $P_n(x)$는 유한 급수가 되어서 모든 점에서 잘 수렴한다.
[참고문헌]
[다음 읽을거리]
1. 구 좌표계의 전자장 표현식
[2] A. M. Legendre, "Recherches sur l'attraction des spheroides homogenes (Research on the attraction of homogeneous spheroids)," Mémoires de Mathématique et de Physique (Memoirs of Mathematics and of Physics), pp. 411–434, 1785.
[다음 읽을거리]
1. 구 좌표계의 전자장 표현식
안녕하세요~ 저는 이 블로그의 내용이 너무 좋아서 휴대폰 인터넷 홈페이지를 이 블로그로 해 놓고 항상 찾아보는 학생입니다. 저는 지금 휴학하고, 전자기학과 전자장론을 다시 보면서 공부하고 있는데요... 제가 공부를 열심히 안해서 그런지 처음부터 보는 그런 느낌입니다..
답글삭제제 소개는 이쯤에서 간략히 하고요, 본문과 관련해서 질문 좀 드리려고 하는데요... 제가 얼마전에 Balanis의 전자장론 책을 보면서, 구좌표계에서 scattering 문제를 다룰 때 르장드르 함수가 쓰이는 것을 알았습니다. 그렇다고 100% 이해한것은 아니고요... 정말 말 그대로 '알았다'는 것입니다.. ㅠㅠ
제가 궁금한 것은 바로 이 르장드르 함수가 물리적으로 어떤 현상을 나타내는 것인가 라는 것입니다. 그러니깐 다시 이걸 설명드리자면... 이 블로그에서 베셀 함수에 관해서 내용을 찾아보다가, 베셀 함수가 천장에 달린 사슬의 운동을 기술하는 과정에서 나온 함수라는 것을 알았습니다. 즉 전자장이 베셀함수로 표현 되어진다면, 그러한 운동과 같은 모습(진동을 하면서, 동시에 감쇠하는... 이랄까요..)이 될 것이라는 게 추측될 수 있을거 같은데요...
그렇다면 르장드르 함수가 나타내는 물리적인 의미는 어떤 것이 있는것입니까? 단지 수학적인 편의성, 편리 때문에 도입이 되진 않았을텐데, 왜 르장드르 함수가 전자장을 표현하는데 꼭 나타나는지 알고 싶습니다.
질문이 너무 어리숙한것 같아 죄송하네요... ㅠㅠ
방문 감사합니다. ^^
삭제르장드르 함수의 시작은 중력장 계산입니다. 점질량인 경우는 $1/r$ 특성을 이용해 중력 포텐셜을 계산할 수 있지만 덩어리로 되어 있다면 적분을 위해 르장드르 함수를 도입한 후 다중극(multipole) 계산을 해야 합니다. 이 부분은 아래 르장드르 함수의 생성함수(generating function)와 관계되어 있다.
$$\frac{1}{\sqrt{1+r^2-2r\cos \phi}} = \sum_{n=0}^{\infty} P_n(\cos \phi) r^n$$
전자장론에서는 이런 부분보다는 말씀하신 구좌표계의 전자장 표현을 위해 사용합니다. 자세한 것은 아래 참고해 보세요. 어렵지만 볼 가치가 충분히 있습니다.
http://ghebook.blogspot.kr/2013/02/electromagnetic-field-representations_10.html
안녕하세요? 전파거북이님 legendre polynomial 관련 포스팅을 보고 댓글을 답니다 다름이 아니라 제가 하려는것은 특정함수 (예를들면 사인함수) 를 다항식으로 전개를 하려고 합니다.
답글삭제전개방법에는 테일러로 다항식으로 전개 할수 있음을 알게 되었는데 테일러는 f(x)=a에서만 근사를 할수 있는것으로 제가 원하는 구간(점이 아님)은 불가능 하다고 판단이 되어서 알아본결과 르장드르 다항식으로는 구간이 가능해 보입니다 사실 이부분도 확실하지 않습니다.
제가 궁금한것은 르장드르 다항식으로 제가 원하는 특정함수를 원하는 구간의 다항식으로 전개가 가능한것인가요?
질문하신 내용은 기저 함수(basis function)의 완비성(completeness)입니다. 테일러 급수와 마찬가지로 르장드르 함수도 완비성이 있어 주어진 구간에 르장드르 함수를 사용할 수 있습니다.
삭제하지만 실제 문제에서는 수렴성이 더 중요합니다. 무한개를 쓰지 않고 적은 수의 기저 함수로 원함수를 근사할 수 있는 지가 매우 중요합니다. 그럴려면 원함수의 특성과 유사한 기저 함수를 택해야 합니다. 즉, 문제마다 적절한 기저 함수가 다를 수 있다는 것이지요.
답변 감사드립니다.
삭제제가 구현하려는 함수는 f(x)=tanh(log(1/x) / log(1/(1+x))) 입니다. 0<x<1
위함수를 수렴하면서 근사 시킬수 있는 방법에 대해서 알고자 합니다.
사실은 이게 꼭 르장드르여야 하는것도 말씀을 들어보면 아닌것 같네요.
혹시 위와같은 함수에서 어떤 기저함수를 택해야하는지 방법같은것이 있을까요?
경험에 의한것이라면 그 경험을 쌓기위해서라도 도전해 보고자 합니다.
그리고 말씀을 보면 꼭 르장드르가 아닌 테일러함수로도 가능한것처럼 보입니다.
제가 생각한게 맞나요?
말씀하신 기저함수는 예를들어 wavelet 의 기저로 cosine이나 daubechies 같은 mother wavelet을 말씀하시는것 같습니다. 하지만 여기서 말씀하신 기저함수는 잘 상상이 안되는데요. 예제의 함수 모형과 비슷한 단일 함수를 의미하시는것인지요? 사실 기저함수에 따른 결과는 wavelet을 실험하면서 그 차이를 많이 경험하였습니다 그래서 말씀하신 기저함수가 중요하다다는것은 알고 있지만 여기서는 러떻게 기저함수를 정하고 원함수에 근사화 할수 있는지 잘 모르겠습니다.
1. 주어진 구간에서 발산하지 않기 때문에 테일러 급수로도 충분히 가능합니다.
삭제2. 고차 르장드르 함수는 수치 해석적으로 구현이 쉽지 않기 때문에 계산을 위해서라면 다른 기저 함수가 좋을 것 같습니다.
3. 수렴성 좋은 함수 근사에 체비셰프 다항식(Chebyshev polynomial)을 이용한 체비셰프 근사(Chebyshev approximation)도 많이 쓰입니다.
전파 거북이님 답변 감사드립니다 그럼 굳이 르장드르를 고집할 필요는 없어 보입니다.
삭제다만 궁금한것이 가급적이면 제가 예시로 드린 함수를 1번이나 3번으로 근사를 할경우 어느것이 더 적고 작은 다항식으로 만들수 있을까요?
그리고 1번에서 답변에서 테일러 함수로도 충분히 수렴을 한다고 말씀을 하신것은 테일러 함수가 -1~1의 범위에서 수렴을 하니까 수렴이 된다고 판단하신것인지 아니면 어떻게 아신건지 궁금하구요
3번같은경우 또 알아봐야 되겠지만 이것도 0과 1사이로 수렴을 할까요?
수렴성을 보려면 근사한 후 부분합과 참값과의 오차를 관찰해야 합니다.
삭제특별한 방법이 있다기 보다는 기저 함수별로 오차를 계산해 빨리 수렴하는 기저 함수로 택하면 됩니다.
테일러 급수는 함수가 특정 영역에서 해석적이면 존재하기 때문에 수렴합니다. 하지만 이게 효율적인 근사는 잘 안되기 때문에 체비셰프 근사와 같이 복잡한 방법을 사용합니다.
전파 거북이님 안녕하세요? 한가지 궁금한것이 있어서 이렇게 문의드립니다
답글삭제함수 합성이라고 해야하나요? 이걸 어떻게 정의하는지 모르겠는데 예를들면 log(x+1)×c 함수를 그냥 그리면 그래프를 logarithm 또는 gamma curve같이 그릴수가 있을텐데요 여기서 저는 c가 커질수록 이 그래프가 s자로 점점.변하게 하고 싶습니다.
이런작업 같은것을 모라고 부르는지는 정확하게 모르겠습니다. 제가 궁금한것은 보통 연구하시는 분들은 이런 작업처럼 자기가 원하는 그래프를 만들기 위해서.처음 뭐를 하고 그다음 어떻게 하는
지가 궁금합니다.
그냥 저같은 일반인입장에서는 c가 커지면 점점 s자가 되게 만들고 싶으니까 log(x+1)에다가 음...뭔가를 곱하면 그런 모양이 될수 있도록 맠드는 함수를 만들어 볼수 있겠습니다만 이경우에는 수만가지 방법이 있을것이고 그중 어껀것이 좋을까 고민하게 될것 같습니다. 사실은 수만가지중에 제대로 나와보이는것을 골라서 그냥 사용 할듯 합니다만.
실제 연구하시는분들은 어떻게 하시는지요?
Ipslab님, 질문 하신 부분은 곡선 맞춤(curve fitting)과 관련이 될 것 같습니다. 곡선 맞춤을 할 때 많은 방법이 있지만 쉽게 하려면 라그랑쥐 보간법(Lagrange interpolation) 정도 쓰면 될 듯합니다.
삭제곡선 맞춤으로 생성한 멱급수를 관찰해서 적당한 고급 함수로 바꾸면 더 멋진 근사식을 만들 수도 있죠.
전파거북이님 안녕하세요. 혹시 르장드르 방정식의 일반해에서 왜 a(n) 을 (2n)!/(2^n(n!)^2) 으로 잡았는지 알 수 있을까요? 전공서적을 읽어보면 이유도 없고 아니면 단순히 이로인해 pn(1) =1 이라는 설명이 있는데 잘 이해가 안되네요!
답글삭제찾아보신 내용이 맞습니다. 르장드르 다항식의 최대값이 1이 되도록 택한 것입니다. 최대값되는 위치 중 하나는 $x = 1$일 때입니다.
삭제음... 제가 큰 틀을 잘 이해하지 못해서 드리는 질문일 순 있지만 왜 최대값을 1로 지정하였고 왜 하필 그 값의 위치가 1인가요?
삭제책을 찾아보아도, 인터넷 서핑을 해도 이 질문에 대한 답은 찾을 수가 없더군요. 근데 제 생각이지만 르장드르 생성함수가 중력장의 계산에 사용된다고 들었는데 혹시 이런 복잡한 자연현상을 수학적으로 해석하기 위해 르장드르가 마치 tool 처럼 이용이 되고 이런 tool를 잘(?)혹은 계산의 단순화, 깔끔함을 위해 Pn(1)=1 은 끼워맞춘 결과인건가요?
삭제정규화를 그렇게 정한 것은 제안자만 알 것이고요. ^^
삭제르장드르 다항식의 역사는 중력장(여기 옛날 댓글에 수식 있음)에서 출발합니다. 이걸로 유추하면 말씀하신 대로 설명할 수 있습니다. 댓글에 있는 수식에 $x = \cos \phi = 1$을 대입하고 이항 정리를 쓰면 $P_n (1) = 1$이 되는 것을 증명할 수 있습니다.
감사합니다~!
삭제공부하는데 정말 도움이 많이되고있습니다 감사합니다
답글삭제방문 감사해요, 익명님. ^^ 많은 성과 만드시길 바래요.
삭제전파 거북이님 자료 감사합니다. 학교 공부하면서 많은 도움이 되고 있습니다.
답글삭제혹시 실례가 되지 않는다면 질문좀 해도 될까요?
지금 제가 뭔갈 잘못 이해 했는지 식 12까지 이해가 되는데 어떻게 해서 식 13이 나오는지 이해가 되질 않습니다.
혹시 왜 13번식이 나오는지 알려주실수 있나요?
Unknown님, 단순하게 생각하시면 됩니다.
삭제차수(degree) $n = 0$이면 짝수를 위한 식 (10)을 이용합니다. 그러면 $P_0(x) = 1$이 됩니다. 차수 $n = 1$이면 홀수를 위한 식 (11)을 이용해 $P_1(x) = x$를 구합니다. 나머지 지표도 동일한 방법으로 구해요. 다만 식 (13)을 이용해 정규화를 해야 합니다.
답변 감사드림니다. 전파거북이님 제가 답변해주신 부분까지 까지는 이해를 했습니다. 하지만 n이 1일때 왜? 저 식이 어떠한 과정으로 나오는지 이해를 하지 못해서 질문을 드렸습니다.
삭제간단히 대입해서 증명을 하려고 했는데 수나 너무 커지고 복잡해져서 따로 계산하는 법이 있는지 에 대해 알고 싶습니다.
삭제Unknown님, 식 (11)에 $n = 1$을 넣으면 $P_1(x) = x$이 바로 나옵니다. 어떤 이유 때문에 복잡해진다고 생각하시나요?
삭제르장드르 다항식은 일반적으로 식 (10)과 (11)로 계산하고, 결과식은 식 (13)처럼 표현합니다. 다만 차수가 커지면 르장드르 다항식의 계산이 어려워져요. 이를 위해서 다양한 계산법이 논문지에 발표되고 있어요.
전파거북이님 자료 잘 봤습니다. 이제 다시 수학을 공부하려 하니 어려운 부분이 많이 생기네요
답글삭제부끄럽지만 질문드려도 될까요?
변수를 변환하는데 있어 (2)번에서 (3)번까지의 과정이 이해가 가지 않습니다
식 (3) 밑에 내용을 조금 더 추가했어요. 그래도 이해가 잘 안되면 삼각 함수의 미분을 보셔야 합니다.
삭제정리를 너무 깔끔하게 해주셔서 공부하면서 너무 도움이 되었습니다. 감사합니다.
삭제안녕하세요. 자연대학부생인데 공부할 때마다 너무 도움이 되서 잘 보고있어요! 정말 감사합니다.
답글삭제궁금한 게 있는데요, 식 23이 나오는 부분이 잘 이해가 가지 않는데.. 21번 식이 4번식을 m번 미분한 식이라서, 4번식의 해를 m번 미분한 것이 21번식의 해이다라는 논리가 잘 이해가 가지 않습니다...ㅠㅠ
식 (20)에 있는 변수 정의를 보세요. 식 (21)은 $y$가 아닌 $u$에 대한 미분 방정식입니다.
삭제안녕하십니까. 좋은 글 감사드립니다.
답글삭제식 (20)에서 y를 u에 대한 식으로 치환해서 새로운 미분방정식을 만들었는데,
이 y와 u에 대한 관계식이 어디서 비롯된 것인지 궁금합니다. 직관적인 것인가요?
위 내용은 미분 방정식의 해법을 소개한 것입니다. 이걸 처음에 한 사람은 아마도 주먹구구로 했을 것 같습니다.
삭제답변 감사합니다.
삭제사랑합니다
답글삭제안녕하세요~ 맨 위의 식에서 m=/=0인 경우는 잘 안나올까요?
답글삭제조건 $m \ne 0$인 미분 방정식의 해는 버금 르장드르 함수입니다.
삭제버금 르장드르 함수는 복잡해서 잘 쓰이지 않지만, 구 좌표계에서 3차원 파동을 표현할 때는 꼭 있어야 하는 함수입니다.