고출력 증폭기인 TWT(Traveling-Wave Tube)

[경고] 아래 글을 읽지 않고 "TWT"를 보면 바보로 느껴질 수 있습니다.
1. 최초의 입자 가속기 사이클로트론

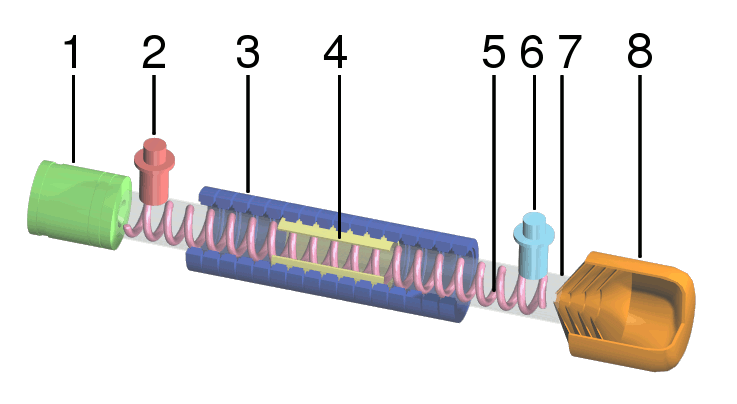
[그림 1] 나선형 TWT의 구조(출처: wikipedia.org)

1: 전자총(electron gun)
2: RF 입력부(RF input)
3: 자석(magnet)
4: 감쇠기(attenuator)
5: 나선형 코일(helical coils)
6: RF 출력부(RF output)
7: 진공관(vacuum tube)
8: 빔 수집기(beam collector)

[그림 1]에 있는 나선형 TWT(helix traveling-wave tube)는 RF(Radio Frequency) 입력을 고출력으로 크게 증폭하기 위해 사용한다. TWT는 진행파관(進行波管)으로 번역하기도 하나, 요즘은 주로 영어 그대로인 TWT를 많이 쓴다. TWT의 구동주파수는 300 MHz~50 GHz이며 분수 대역폭(fractional bandwidth: $f_H/f_L$)은 2 정도이다. 분수 대역폭은 대역폭에서 가장 높은 주파수($f_H$)를 가장 낮은 주파수($f_L$)로 나눈 값이다. TWT의 가능한 이득(gain)은 약 70 dB이다.

TWT의 동작 원리는 단순하다. 전자총[그림 1의 1]이 뜨거워져 열 전자 방출(thermionic emission)이 시작되면 양극(anode: 그림 1의 1)에 가해진 전압에 의해 전자(electron)는 고속으로 움직인다. 전자가 움직이는 방향을 $z$축이라 가정하자. 운동 전자가 중앙으로 잘 집속이 되도록 자석[그림 1의 3]의 자기장(magnetic field)을 $z$축으로 걸어준다.[∵ 사이클로트론(cyclotron) 원리에 의해 자기장이 강하게 걸리면 구심력(centripetal force)이 커지므로 움직일 수 있는 반지름이 줄어든다.] 진공관[그림 1의 7)을 통과한 전자는 빔 수집기[그림 1의 8]에 수집된다. 이를 위해 빔수집기에는 약 1 kV의 전압을 건다. RF 입력부에 특정 주파수의 전자파를 집어넣으면 이 전자파는 전자총에서 나온 전자와 상호 작용한다. 상호 작용은 별개 아니고 전자가 전자파의 전기장(electric field)과 전기력(electric force)을 주고 받는다는 뜻이다. 여기서 나선형 코일[그림 1의 5]은 전자파를 이송하는 전송선(transmission line) 역할을 한다. 전자와 전자파가 정상적인 상호 작용을 하기 위해서는 동기(synchronism)가 맞아야 한다[1]. 상호 작용 관계식을 유도하기 위해 전자파의 위상을 고려하자.

                            (1)

여기서 $k_z$는 전송선의 $z$방향 위상 상수(phase constant), $v_z$는 전자의 $z$방향 속도, $f$는 RF의 주파수이다. 식 (1)은 전자파의 이동 속도[= $v_p$ = $\omega/k_z$]와 전자의 이동 속도[= $v_z$]가 동기가 됨을 의미한다. 또한 전자가 가진 에너지가 전자파로 옮겨지기 위해서는 위상이 시간적으로 변해서는 안된다.

[그림 2] 전자의 뭉침 현상(출처: [1])

식 (1)의 조건이 만족되면 [그림 2]와 같이 $z$축 방향으로 전자의 뭉침 현상(electron bunching)이 나타난다. 전자는 한 방향으로만 움직이고 있지만 전자파는 관내 파장(guided wavelength) 특성으로 인해 전기장의 세기가 [그림 2]처럼 바뀐다. 전기장이 가해진 방향을 $z$축이라 하면[예를 들면 $\bar E = E_0 \hat z$] 전기장이 (-)인 위치에서는 전자가 가속되고 전기장이 (+)인 위치에서는 전자가 감속된다. 이로 인해 전자는 특정 위치에 뭉쳐지게 된다. 식 (1)을 만족하려면 전자파와 전자의 이동 속도가 같아야 한다. 하지만 전자는 속도($v_z$)를 아무리 높여도 광속($c$)을 넘어설 수 없기 때문에, 전자파의 속도($v_p$)를 줄여 식 (1)을 만족시켜야 한다. 그래서 [그림 1]의 5가 표현하는 TWT의 전송선을 설계할 때는 저속 파동(slow-wave) 조건을 고려한다.

                            (2)

하지만 통상적인 전송선으로 식 (2)를 만족시킬 수 없다. 도파관(waveguide)은 고속 파동(fast-wave: $v_p > c$)이기 때문이다. 이 문제를 해결하기 위해 나선형 코일과 같은 주기 구조를 가진 전송선(periodic transmission line)을 사용한다. 전송선이 $z$방향으로 주기성을 가지면 플로케 정리(Floquet theorem)에 의해 $k_z$는 아래식을 만족한다.

                            (3)

여기서 $L$은 주기 구조의 주기이다. 따라서 전송선을 따라 전자가 이동하면 전자 뭉침이 더욱 강해진다. 강해진 전자 뭉침은 강해진 RF 혹은 증폭된 RF를 뜻한다. 이때 생긴 전자 뭉침의 주기는 RF 출력부에 나오는 RF 출력 주파수와 같다. [그림 2]를 다시 보자. 전자파와 전자의 이동 속도가 같으면 전자의 뭉침은 일어나지만 전기장이 0인 지점에 뭉쳐지므로 전자의 에너지가 전자파의 에너지로 변환되지 않는다.[∵ 에너지(energy)가 생기려면 힘(force)이 필요하다. 하지만 전기장이 0이면 전기력도 0이 된다.] 그래서, 실제 TWT를 만들 때는 전자의 속도가 전자파의 속도보다 약간 빠르게 만든다. 그러면 전자 뭉침의 중심(center of bunch)은 [그림 2]처럼 전기장이 (+)가 되는 지점[혹은 전자가 감속되는 지점]에 생겨 에너지 전달이 일어나게 된다. 이를 이해하려면 힘과 에너지 관계를 보면 된다. 전하량이 (-)인 전자에 전기장이 (-)로 걸리면 전자는 $+z$로 향하는 전기력을 받는다. 즉, 전자가 에너지를 얻는다. 반대로 전기장이 (+)로 걸리면 전자는 감속을 받아 운동 에너지(kinetic energy)가 작아지고 이때 생긴 여분의 에너지는 다른 에너지로 변환되어야 한다. 전자가 감속되면 전자파 복사(electromagnetic radiation)가 일어나야 하므로, 전자의 운동 에너지는 RF 에너지로 바뀌게 된다. 다른 관점으로 한 번 보자. 전자가 전자파보다 약간 빠른 속도를 가지면 그 속도차 만큼이 RF 에너지가 된다. 왜냐하면 전자 뭉침의 중심이 감속 구간에 있어 전자가 느려지기 때문이다. 전자가 느려지다가 전자파와 같은 속도가 되면 더이상의 에너지 변환은 일어나지 않는다. 하지만, 전자총([그림 1]의 1)에서 계속 고속 전자를 방출하기 때문에 운동 에너지가 계속 공급되어 지속적으로 RF 에너지로 변환된다.

[그림 1]에 있는 감쇠기[그림 1의 4]는 중요한 역할을 한다. [그림 1]과 같은 구조에서 RF 출력을 빼내면 RF 신호의 반사(reflection)가 생길 수 있다. 이때 생긴 반사 성분이 좌우로 무한히 반사하면서 원치않는 공진(resonance)을 만들 수 있기 때문에, 강제적으로 전자파 감쇠를 주어 공진이 생기지 않도록 한다. TWT는 증폭기(amplifier)이므로 주변에 커패시터(capacitor)와 인덕터(inductor)를 잘 붙이면 발진기(oscillator)로 쓸 수도 있다. 발진기는 RF 입력없이 특정한 주파수의 RF 출력을 안정적으로 만들 수 있는 회로 소자이다. 정확하게는 우리가 가한 RF 입력이 없을 뿐 잡음(noise)이 RF 입력 역할을 한다. 또한 GHz 이상에서는 좋은 커패시터와 인덕터는 없기 때문에, 전송선(transmission line)의 입력 임피던스(input impedance)를 이용해 등가적으로 커패시터와 인덕터를 만들어 초고주파 발진기를 설계할 수 있다.

[그림 3] 지대공 무기 체계 천마(출처: ko.wikipedia.org)

[그림 3]에 있는 우리나라에서 자체 개발한 지대공(地對空, Surface-to-Air) 무기 체계인 천마(天馬, Pegasus)의 추적 레이다(tracking radar)가 TWT를 전자파 원천(electromagnetic source)으로 사용한다. 레이다의 전자파 원천으로 TWT와 같은 고출력 발생기를 채택하면 레이다의 탐지 거리가 획기적으로 향상된다.

[참고문헌]

[1] K. R. Chu, "The electron cyclotron maser," Rev. Mod. Phys., vol. 76, no. 2, pp. April 2004.

[다음 읽을거리]
1. 주파수 안정성이 좋은 클라이스트론
2. 고출력 밀리미터파 생성 위한 자이로트론