1. 텐서
2. 행렬
3. 행렬식
벡터(vector) 혹은 행렬(matrix)과 분명히 구별되는 텐서(tensor)의 특성은 좌표 불변(座標獨立, coordinate independent or coordinate invariant)이다. 텐서의 좌표 불변성을 좌표 변환(座標變換, coordinate transform) 관점으로 생각해본다. 최초의 좌표계(座標系, coordinate system)이자 우리 직관과도 잘 일치하는 좌표계는 [그림 1]의 데카르트 좌표계(Cartesian coordinate system)이다.

[그림 1] 2차원과 3차원 데카르트 좌표계(출처: wikipedia.org)
[그림 2] 1차원 데카르트 좌표계의 측도 표현(출처: wikipedia.org)
측도는 길이를 재는 단위(unit interval)이다. 예를 들어 [그림 2]는 1이라는 측도로 무한히 좌우로 연결하면 1차원 데카르트 좌표계 $(x)$가 됨을 보여준다. 가로 방향에 수직 방향인 세로 방향으로 좌표축을 확장하면 [그림 1]의 왼쪽에 있는 2차원 데카르트 좌표계 $(x, y)$를 생성할 수 있다. 마찬가지로 [그림 1]의 오른쪽처럼 높이 방향으로 확장하면 3차원 데카르트 좌표계 $(x, y, z)$가 얻어진다. 우리가 쉽게 상상할 수 있는 데카르트 좌표계를 좌표 변환의 기준 좌표계라고 보통 생각한다.

[그림 3] 근방의 개념(출처: wikipedia.org)
좌표계의 차원은 3차원이라 가정해도 큰 문제가 없으므로[∵ 차원 확장은 좌표점을 구성하는 좌표의 수를 늘리면 쉽게 되므로] 데카르트 좌표계 $X$ = $(x^1, x^2, x^3)$에서 일반 좌표계(generalized coordinate system or curvilinear coordinate system) $U$ = $(u^1, u^2, u^3)$로 가는 일반적인 좌표 변환을 아래로 정의한다.
 (1)
(1)
텐서에서 말하는 좌표 변환은 기저 벡터(basis vector)의 변경이라 생각하면 쉽다. 예를 들어 벡터(vector) $\bar A$는 데카르트 좌표계에서는 $\bar A(x,y,z)$ = $A_x(x,y,z) \hat x + A_y(x, y, z) \hat y + A_z(x, y, z) \hat z$로 표시할 수 있다. 하지만 좌표 변환한 원통 좌표계(circular cylindrical coordinate system)에서는 동일한 벡터를 $\bar A(\rho, \phi, z)$ = $A_\rho (\rho, \phi, z) \hat \rho + A_\phi (\rho, \phi, z) \hat \phi + A_z (\rho, \phi, z) \hat z$로 표현한다. 비슷하게 구 좌표계(spherical coordinate system)에서는 $\bar A(r, \theta, \phi)$ = $A_r (r, \theta, \phi) \hat \rho + A_\theta (r, \theta, \phi) \hat \theta + A_\phi (r, \theta, \phi) \hat \phi$처럼 쓸 수 있다. 또한 위치 벡터(position vector)는 텐서를 구성 못할 수도 있으므로,[∵ 좌표계의 원점이 다르면 위치 벡터는 서로 달라진다.] 식 (1)에 있는 위치 벡터의 차이를 텐서로 정의해야 함에 주의한다. 위치 벡터의 차이를 한없이 줄여가면 좌표계의 미분(differential)을 아래처럼 정의할 수 있다.
 (2)
(2)
여기서 $i$는 자유 첨자(free index: 합 기호에서 한 번만 출현하여 텐서가 표현하는 방정식을 명확히 표시), $j$는 무효 첨자(dummy index: 합 기호에서 두 번 출현하여 합 기호가 생략됨을 표시, 자유 첨자와 같지 않으면 다른 문자로 변경 가능), 동일한 지표(指標, index: 식 (2)에서 $j$)가 반복되어 합 기호(summation symbol) $\Sigma$를 생략하면 아인슈타인 표기법(Einstein notation)이라 한다. 즉, 곱해진 기호에서 동일한 지표가 출현하면 합 기호 $\Sigma$가 있다고 생각해야 한다. 텐서 이론에서는 아인슈타인 표기법을 거의 사용하기 때문에 식 (2)에 익숙해져야 한다. 식 (2)의 미분 개념이 유용한 이유는 [그림 3]의 근방(近方, neighborhood) 관점으로 생각할 수 있다. 미분은 한없이 작아지는 두 지점을 의미하기 때문에 특정한 점 $P$의 3차원에 대한 미분을 [그림 3]에 있는 근방이라 생각할 수 있다. 이 근방을 모두 합치면 3차원 공간을 모두 만들 수 있다. 즉, 좌표계간의 일반적인 좌표 변환을 식 (2)를 이용해 표현할 수 있다. 하지만, 식 (2)가 성립하기 위해서는 아래 관계식이 반드시 성립해야 한다.
 (3)
(3)
식 (3)에 나오는 결과는 유명한 야코비 행렬식(Jacobian determinant or Jacobian)이다. 여기서 야코비 행렬식은 야코비 행렬(Jacobian matrix) $\bf J$의 행렬식[= $|{\bf J}|$]이다. 예를 들어 2차원인 경우 야코비 행렬 $\bf J$는 식 (4)로 표현할 수 있다.
 (4)
(4)
여기서 $\bf J$는 $(x, y)$에서 $(x', y')$로 가는 좌표 변환에 사용한다. 이는 식 (4)의 야코비 행렬을 만들 때 좌표 성분 $x' = x'(x, y)$와 $y' = y'(x, y)$를 $x$와 $y$에 대해 편미분하기 때문이다. 식 (2)에 있는 데카르트 좌표계 $X$의 미분[혹은 근방] $dx$와 일반 좌표계 $U$의 미분[혹은 근방] $du$가 식 (1)의 좌표 변환을 통해 상호 연결되기 위해서는 식 (3)의 야코비 행렬식이 0이 아니어야 한다. 행렬식이 0이 아니면 식 (4)의 역행렬(inverse matrix)이 존재해서 $dx$와 $du$가 식 (4)의 행렬 관계를 통해 서로 종속적이 되도록 변환할 수 있다. 즉, 식 (4)를 통해 $dx$는 $du$를 만들 수 있고 식 (4)에 있는 야코비 행렬의 역행렬을 만들어 $du$가 $dx$를 생성하도록 할 수 있다. 이를 정리하면 아래와 같다.
일반 좌표계간의 좌표 변환이 일대일 대응(一對一對應, one-to-one mapping)이 되기 위해서는 좌표 변환의 야코비 행렬식이 0이 아니어야 한다.

[그림 4] 공변 벡터와 반변 벡터(출처: wikipedia.org)
또한, 좌표계가 만들어지기 위해서는 좌표계를 구성하는 벡터(vector)가 정의되어야 한다. 텐서 이론에서는 두 가지 종류의 기저 벡터(basis vector)를 [그림 4]와 같이 정의한다.
 (5: 공변 기저 벡터)
(5: 공변 기저 벡터) (6: 반변 기저 벡터)
(6: 반변 기저 벡터)
식 (5)에 있는 일반 좌표계 $U$의 위치 벡터는 아래로 정의한다.
 (7)
(7)
여기서 $O$는 데카르트 좌표계 $X$의 원점이며 좌표 변환이 정해지면 고정된다.[미분 관점에서 좌표점 $O$는 고정되었기 때문에 없는 것과 마찬가지이다.] 또한, 일반 좌표계 $U$에서는 위치 벡터지만 데카르트 좌표계 $X$에서는 위치 벡터의 차이로 정의함을 눈여겨 봐야한다. 텐서가 되려면 좌표 불변성을 만족해야 하기 때문에 식 (7) 정의를 따라야 한다. 식 (5)는 좌표축의 기저 벡터(basis vector)를 정의할 때 사용하는 일반적인 방법이다. 예를 들어 데카르트 좌표계의 기저 벡터는 아래식으로 얻을 수 있다.
 (8)
(8)
식 (5)를 수식적으로만 보면 위치 벡터 $\bar r$을 $u^i$ 방향으로 편미분하라는 의미이다. 그러면 $u^i$가 변하는 방향을 나타내는 벡터가 얻어진다. 즉, $u^i$축을 표현하는 벡터가 된다. 식 (6)은 변환 $u^i$에 대한 구배(gradient)이다. 구배 연산자는 정상[꼭대기] 검출기이기 때문에 $u^i$가 최대로 변하는 방향을 얻을 수 있다. 데카르트 좌표계에서는 식 (5)와 (6)의 벡터는 서로 동일하다.[$u^1 = x$, $u^2 = y$, $u^3 = z$라 가정해서 식 (6)에 대입해보라.] 하지만 일반 좌표계인 경우는 같을 필요가 없다. 식 (5)와 (6)에 제시한 벡터의 관계식을 얻기 위해 내적(inner product)을 취한다.
 (9)
(9) and
and  (10)
(10)
신기하게도 벡터의 내적인 식 (9)는 식 (10)으로 표현되는 크로네커 델타(Kronecker delta)가 된다. 식 (9)에서 $u^i$의 편미분이 크로네커 델타가 되는 이유는 무엇일까? 바로 편미분의 정의 때문이다. 편미분에서는 내가 관심있는 변수[식 (9)에서 $u^j$]가 아니면 모두 상수로 취급하므로 $i \ne j$인 경우는 상수 취급되어 모두 0이 된다.
좀더 엄밀하게 식 (5)와 (6)의 벡터를 표현하면, 식 (5)는 공변 벡터(共變, covariant vector or covector), 식 (6)은 반변 벡터(反變, contravariant vector: 흔히 벡터라고 함)라고 한다. 공변 벡터는 다른 말로 미분 형식(differential form) 혹은 1차 형식(one-form: 단순하게 생각하면 텐서 생성시 벡터를 하나만 사용한 형식이며, 1차 형식의 원래 정의는 벡터에서 좌표 성분을 뽑는 함수 관계이다.)[1]이라 한다. 식 (5)와 (6)처럼 텐서에서는 공변과 반변을 나타내기 위해 아래첨자(subscript, lower index)와 위첨자(superscript, upper index)를 사용한다. 수학적으로만 보면 $\partial x^j / \partial u^i$로 표현되면 공변 특성, $\partial u^j / \partial x^i$라면 반변 특성이 된다. 즉, 식 (5)에 있는 $\partial x^j / \partial u^i$는 데카르트 좌표계 $X$가 있고, 이 성분을 일반 좌표계 $U$의 성분 방향으로 미분한다는 뜻이다. 이는 $X$에서 $U$로 가는 좌표 변환 특성을 표현하고 있으므로 공변[좌표 변환과 비례]이 된다. 반면 반변[좌표 변환과 반비례]은 $\partial u^j / \partial x^i$가 되어, 공변과는 거꾸로 $U$ 성분을 $X$ 성분 방향으로 미분하는 특성을 표현한다. 미분 연산자 관점으로 보면 식 (5)와 (6)이 공변과 반변을 표현하는 의미를 더 쉽게 생각할 수 있다. 공변 미분 연산자는 $\partial x^j / \partial u^i \cdot \partial / \partial x^j = \partial / \partial u^i$처럼 변환된다.[분명 미분 연산자는 $X$에서 $U$로 갔다.] 반변은 $\partial u^j / \partial x^i \cdot \partial / \partial u^j = \partial / \partial x^i$이다.[반변은 $U$에서 $X$로 갔다.] 좌표 변환[$X \to U$]에 대해 함께 변하는 공변과 거꾸로 변하는 반변 특성이 미분 연산자 변환에서 잘 나타난다. 예를 들어 $u^i = 2 x^i$인 좌표 변환에서, $\bar a_i$는 $X$의 위치 벡터를 $U$ 성분으로 미분해 공변 특성인 $1/2 \cdot \hat x_i$가 된다. 반변은 공변과 반대되므로, $\bar a^i = 2 \hat x_i$가 얻어진다. 이 결과를 벡터 성분 관점에서 본다. $X$ 좌표계에서 $A \hat x_i$인 벡터는 공변과 반변 기저 벡터 관점에서 $A \hat x_i$ = $(2A) (1/2 \cdot \hat x_i)$ = $(1/2 \cdot A) (2 \hat x_i)$로 각각 표현된다. 즉 좌표 변환[$X \to U$]에 대해 함께 변하는 공변과 거꾸로 변하는 반변 특성을 벡터 성분에서 관찰할 수 있다.
공변[위치 벡터의 $u^i$ 편미분 방향]과 반변[등치면(isosurface) $u^i$의 최대 변화 방향] 벡터 관계는 어떤 좌표축의 접선과 수직 성분 관계가 아니다. 예를 들면 반변 벡터는 데카르트 좌표에서 $\hat x$로 정하고, 공변 벡터는 $\hat x$에 수직인 $\hat y$ 혹은 $\hat z$ 중 하나로 정하지는 않는다. 물론 이렇게 될 수도 있지만 일반론을 말한다. 오히려 공변과 반변 벡터는 반드시 좌표 변환 관점에서 생각해야 한다. 단순히 서로 접선과 수직 관계로 공변과 반변 벡터를 정의하면 데카르트 좌표계에서 공변과 반변 벡터가 동일한 이유가 설명되지 않는다. 예를 들어 식 (5)와 (6)에서 $u^1 = x^1$라 두면 $\bar a_1$ = $\bar a^1$ = $\hat x$가 되어 공변과 반변이 특정 좌표축에 접선과 수직이 아님을 알 수 있다.[∵ 동일한 방향이므로 특정 좌표축에 접함과 수직이 동시에 될 수 없다.] 그래서 공변과 반변은 단어 의미 그대로 미분 연산자나 기저 벡터의 변환이 좌표 변환과 정비례로 변하는지 혹은 반비례로 변하는지를 의미한다.
여기까지 이해했다면 이 부분도 생각한다. 텐서에서는 왜 이렇게 복잡하게 벡터를 정의하는가? 바로 동일한 물리적 현상을 다른 좌표계에서 보기 위해서이다.[텐서는 임의의 기하 구조를 좌표 독립적으로 표현하기 위한 표기법임을 기억한다.] 좌표 변환을 한다면 그 특성은 비례 혹은 반비례 특성을 가진다. 여기에 벡터적 특성을 도입하여 공변[좌표 변환과 비례]과 반변[좌표 변환과 반비례]으로 표현한다. 물론, 식 (9)의 증명처럼 공변과 반변 벡터는 기하학적으로 서로 수직인 중요한 성질도 있다. 또한 공변 벡터와 반변 벡터의 중요한 특징은 좌표 변환의 일대일 대응 조건인 식 (3)에 있다. 야코비 행렬식이 0이 아니기 때문에 공변 벡터는 서로 독립이다. 마찬가지로 반변 벡터도 서로 독립이다. 이를 이해하려면 식 (3)에 있는 야코비 행렬을 식 (11)과 같이 반변 벡터와 공변 벡터로 표현하면 된다.
 (11)
(11)
식 (11)로 표현된 야코비 행렬의 행렬식이 식 (3)에 의해 0이 아니기 때문에 당연히 서로 독립이다. 즉, 좌표계를 표현하는 기저 벡터로 사용할 수 있다. 또한, 식 (9)와 식 (11)을 연결하면 식 (11)에 있는 야코비 행렬은 서로 역행렬 관계임을 쉽게 알 수 있다.
 (12)
(12)
즉 일반화된 좌표계에서는 기저 벡터가 서로 수직이 아니므로 사용하기가 무척 불편하다. 하지만 이를 공변 벡터와 반변 벡터로 표현하면, 식 (12)나 식 (15)에 의해 공변 벡터와 반변 벡터는 서로 수직이므로 직교성(orthogonality)을 이용해서 좀더 편하게 일반화된 좌표계를 다룰 수 있다.
식 (5)와 완전 미분(exact differential)을 이용해 위치 벡터의 미분 $d \bar r$을 공변 벡터 관점에서 정의한다.
 (13)
(13)
식 (13)에서 $du^i$는 공변 벡터를 위한 미분소이지만 반변으로 표현했다. 왜냐하면 식 (9)에 의해 반변 벡터를 식 (13)과 내적하면 반변 성분인 반변 미분소가 얻어지기 때문이다. 식 (13)과 비슷한 방식으로 동일한 위치 벡터의 미분 $d \bar r$을 반변 벡터 관점에서 정의할 수 있다. 또한 식 (13) 이전까지는 위치 벡터 정의를 위해 반변 좌표 성분인 $u^i$를 사용했지만, 식 (13)의 쌍대(duality)를 얻기 위해 공변 좌표 성분 $u_i$의 도입이 필요하다. 이를 종합하여 위치 벡터의 미분 $d \bar r$을 새롭게 정의하면 다음과 같다.
 (14)
(14)
여기서 $du_i$는 공변 성분을 표현하는 공변 미분소이다. 식 (13)과 (14)는 각각 공변 및 반변 벡터 표현식(covariant and contravariant vector representations)으로 간주할 수 있다. 식 (14)에 나온 공변 미분소 $du_i$를 계산하기 위해 아래 관계식을 고려한다.
 (15)
(15)
여기서 $g^{ij}, g_{ij}$는 계량 텐서(metric tensor)이다. 식 (15)의 첫째 식을 보면 어떤 반변 기저 $\bar a^i$는 다른 공변 기저 $\bar a_j$에 항상 수직이다. 예를 들면 $\bar a^1$은 $\bar a_2$와 $\bar a_3$에 수직이다. 평면 방정식 관점으로 보면, 기저 벡터 $\bar a_2$와 $\bar a_3$가 만드는 평면은 항상 $\bar a^1$에 수직이다. 마찬가지로 $\bar a_1$은 $\bar a^2$와 $\bar a^3$에 수직이며, 기저 벡터 $\bar a^2$와 $\bar a^3$로 표현한 평면은 $\bar a_1$에도 수직이다. 계량 텐서를 이용하면 공변과 반변 미분소를 식 (15)처럼 서로 변환할 수 있다. 식 (5), (6), (15)를 이용해 계량 텐서를 구하면 아래와 같다.
 (16a)
(16a) (16b)
(16b)
식 (16)이 거리를 측정할 수 있는 계량 텐서인 이유는 선미분소 $ds$를 아래와 같이 계산해보면 분명히 알 수 있다.
 (17)
(17)
[그림 5] 데카르트 좌표계의 거리(출처: wikipedia.org)
데카르트 좌표계 $X$에서 일반 좌표계 $U$로 가는 좌표 변환 중 $U$가 데카르트 좌표계인 경우의 계량 텐서는 식 (16)에 의해 크로네커 델타가 된다. 그러면 선미분소는 [그림 5]처럼 우리가 잘 아는 피타고라스의 정리(Pythagorean theorem)를 만족하게 된다.
 (18)
(18)
계량 텐서의 성질은 식 (17)을 바탕으로 아래와 같이 증명할 수 있다.
 (19)
(19) (20)
(20)
이상의 논의를 바탕으로 임의의 좌표계에서 표현된 텐서가 좌표 불변성을 갖는지 증명한다. 벡터 $\bar A$는 일반 좌표계 $U$에서 정의되고 벡터 $\bar B$는 일반 좌표계 $V$에서 정의된다고 가정한다. 식 (2)와 (5)를 이용하여 식 (13) 형태의 공변 벡터 표현식으로 벡터 $\bar A, \bar B$를 표현하면 다음과 같다.
 (21)
(21)
식 (21)에 완전 미분의 특성을 적용하면 벡터 $\bar A, \bar B$가 등가임을 보일 수 있다.
 (22)
(22)
식 (22)가 성립하기 때문에 텐서 개념을 좀더 확장할 수 있다. 지금까지 논의에서 좌표 변환의 출발점은 데카르트 좌표계 $X$로 한정했지만, 더 일반화해서 임의의 일반 좌표계 $U$에서 $V$로 가는 좌표 변환을 텐서 관점으로 고려할 수 있다. 식 (9)에 있는 반변 벡터와 공변 벡터의 관계식도 일반화할 수 있다.
 (23)
(23)
즉 일반 좌표계 $U$에서 식 (9)가 성립하면, 식 (23)에 의해 일반 좌표계 $V$에서도 식 (9)와 같은 관계가 자동적으로 얻어진다.
그러면 벡터와 유사한 1차 텐서(1st order tensor)를 일반화하여 혼합 텐서(mixed tensor)를 정의한다. 1차 텐서를 표현한 식 (5)와 (6)과 유사하게 고차 텐서를 정의하면 다음과 같다.
 (24)
(24)
식 (24)가 복잡해 보이는가? 어렵게 생각할 필요없다. 식 (5)와 (6)처럼 표현되면 텐서량이 되기 때문에 고차 텐서도 식 (24)처럼 표현되어야 한다고 생각하라. 혼합 텐서는 공변 텐서(covariant tensor)와 반변 텐서(contravariant tensor)의 곱이기 때문에 식 (24)를 아래식으로 분해해서 표현할 수 있다.
 (25)
(25)
여기서 $U, X$는 반변 텐서이며 $V, Y$는 공변 텐서이다. 식 (24)와 (25)를 이용해서 텐서의 연산 몇 가지를 예로 들면 아래와 같다.
 (26)
(26)
식 (26)에 제시된 대로 텐서 연산은 덧셈, 뺄셈, 곱셈만으로 구성된다. 벡터에 나눗셈이 정의되지 않는 이유, 행렬간의 나눗셈이 없는 이유[행렬 연산에서는 직접 나눗셈을 하지 않고 역행렬을 계산하여 곱셈으로 처리]와 마찬가지로 텐서는 나눗셈을 정의하지 않는다. 텐서의 나눗셈이 없더라도 식 (15)와 (20)을 이용하여 곱셈을 이용해서 나눗셈과 유사한 연산을 할 수 있다. 즉, 식 (15)에 있는 공변과 반변 개념이 필요한 이유가 나눗셈을 대체하기 위해서이다. 텐서 개념을 이용해 벡터 내적(inner product)을 다시 정의하면 아래와 같다.
 (27)
(27)
식 (27)처럼 동일한 지표를 가진 1차 공변 텐서와 반변 텐서를 서로 곱하면 0차 텐서인 스칼라가 얻어진다. 식 (27)의 과정은 축약(contraction)이라 한다. 텐서에서는 동일한 지표를 가진 공변 텐서와 반변 텐서를 곱하면 항상 텐서의 차수가 낮아지는 축약이 일어난다. 그래서, 공변 텐서와 반변 텐서는 서로 나눗셈 관계에 있다고 생각할 수 있다.[∵ 일반적으로 공변 텐서끼리 혹은 반변 텐서끼리 서로 곱하면 식 (26)처럼 텐서의 차수가 증가한다. 그래서, 텐서의 차수가 감소하면 나눗셈처럼 생각할 수 있다.]
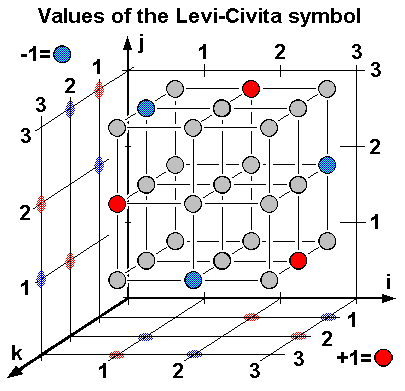
[그림 6] 3차원 레비-치비타 기호(출처: wikipedia.org)
벡터 외적(outer product)은 아래처럼 조금 복잡하다.
 (28)
(28)
식 (28)의 계산에서 공변 벡터에 대응하는 새로운 반변 벡터를 아래처럼 정의한다.
 (29)
(29)
식 (29)가 적절한 이유는 식 (15)에 있다. 예를 들어 공변 벡터 $\bar a_2$와 $\bar a_3$의 외적은 공변 벡터 $\bar a_2$와 $\bar a_3$에 수직이며 공변 벡터 $\bar a_1$과 관련된 어떤 벡터를 만든다. 또한 식 (15)에 의해 공변 벡터 $\bar a_1$과 반변 벡터 $\bar a^1$은 평행인 성분을 가지고 있고 반변 벡터 $\bar a^1$은 공변 벡터 $\bar a_2$와 $\bar a_3$에 수직이므로, 식 (29)의 정의는 완전히 타당하다. 그런데 식 (6)과 (28)에 정의한 반변 벡터는 서로 등가인가 아니면 차이가 나는가?
[공변 벡터와 반변 벡터의 유일성]
반변 벡터가 주어지면 크로네커 델타 관계를 만족하는 공변 벡터는 유일하게 정의된다. 공변 벡터가 주어진 경우에도 동일하다.
[증명]
식 (6)의 반변 벡터를 $\bar a^j$, 식 (28)의 반변 벡터를 $\bar b^j$로 정한다. 식 (23)이 성립하기 때문에 아래가 얻어진다.
 (30)
(30)
식 (30)이 성립하기 위해서는 반변 벡터 $\bar a^j, \bar b^j$가 서로 같아야 한다. 왜냐하면 모든 공변 벡터 $\bar a_i$에 대해 어떤 반변 벡터가 항상 수직일 수는 없기 때문이다.[혹은 어떤 반변 벡터든지 모든 공변 벡터의 선형합으로 표현할 수 있기 때문이다.] 즉, 모든 공변 벡터 $\bar a_i$에 대해 내적이 0인 반변 벡터는 영 벡터가 된다. 반변 벡터가 주어진 경우에도 식 (30)과 유사한 방법으로 공변 벡터가 유일함을 증명할 수 있다.
______________________________
식 (29)를 이용하면 반변 벡터에 대응하는 공변 벡터를 정의할 수 있다.
 (31)
(31)
예를 들어 공변 벡터 $\bar a_3$은 벡터 삼중적(vector triple product)을 사용해서 다음처럼 계산한다.
 (32)
(32)
식 (28)의 벡터 외적을 효과적으로 표현하기 위해 [그림 6]과 같은 레비-치비타 기호(Levi-Civita symbol) $\varepsilon_{ijk}$를 도입하였다.
 and
and  (33)
(33)
여기서 레비-치비타는 수학자 두 명의 이름이 아니다. 이탈리아 수학자인 레비-치비타Tullio Levi-Civita(1873–1941) 한 명의 이름이다. 식 (33)에 제시한 레비-치비타 기호는 행렬식(determinant) 정의에 사용한 순열(permutation) 개념과 동일하다. 즉, 행렬식의 부호함수가 짝수 순열(even permutation)이면 1을 택하고 홀수 순열(odd permutation)이면 -1을 택하는 방식처럼 $\varepsilon_{ijk}$의 순열도 식 (33)처럼 택한다. 레비-치비타 기호는 단순한 기호 같지만 공간의 기하학적 구조를 만들어주는 중요한 기호이다. 레비-치비타 기호가 포함된 식 (28)의 벡터 외적 의미를 생각해보면 이해가 된다. 예를 들어 $x$축 벡터와 $y$축 벡터를 외적하면 새로운 공간축인 $z$축 벡터가 얻어진다. 어떤 종류의 공간구조가 얻어지는지는 식 (33)이 설명해준다. 레비-치비타 기호를 활용하면 3차원을 초과하는 공간의 외적을 쉽게 정의할 수 있다. 레비-치비타 기호는 기본적으로 순열의 부호 함수(sign function)이기 때문에 아래식이 성립한다.
 (34)
(34)
아래 크로네커 델타와 관계된 항등식도 레비-치비타 기호의 재미있는 성질이다.
 (35)
(35)
식 (35)를 증명하기 위해 식 (35)에 있는 모든 지표를 변경하여 좌변과 우변이 같음을 보일 수 있지만 이미 증명된 벡터 항등식 (36)을 이용한다.
 (36)
(36)
식 (27)과 (28)을 이용해 좌변과 우변을 비교하면 식 (35)가 증명된다.
 (37)
(37)
식 (24)는 텐서의 정의이므로 어떤 양이 텐서량인가 보려면 이 양이 식 (24)처럼 표현됨을 확인하면 된다. 예를 들어 식 (16)의 계량 텐서는 아래와 같이 식 (24)에 제시한 형태이므로 2차 텐서이다.
 (38)
(38)
텐서의 좌표 불변성을 이용하여 식 (38)을 아래와 같이 유도할 수도 있다.
 (39)
(39)
텐서의 대수적 특징은 행렬(matrix)과 매우 비슷하다. 텐서는 교환 법칙(commutative law)이 성립하지 않고 결합 법칙(associative law)과 분배 법칙(distributive law)은 성립한다. 이는 행렬을 확장한 개념이 텐서라고 생각하면 쉽게 이해된다.[거듭 강조하지만 텐서는 반드시 좌표 불변성 혹은 좌표 독립성이 성립해야 한다.] 예를 들면 아래의 연산 관계가 성립한다.
 (40)
(40)
식 (40)을 더 쉽게 보려면 n애드(n-ad: $n$개의 항을 연속으로 곱함, 항이 2개인 경우 다이애드) 개념을 아래와 같이 이용하면 된다.
 (41)
(41)
텐서는 식 (40)과 같이 교환 법칙이 성립하지 않지만 식 (2)의 아인슈타인 표기법을 이용한 식 (27)과 같은 텐서 축약 계산에서는 합 기호[= $\Sigma$] 안의 숫자 위치를 바꿀 수 있다.[∵ 당연히 숫자니까 위치를 바꿀 수 있다.] 예를 들면 당연히 아래식이 성립한다.
 (42)
(42)[참고문헌]
[1] growscience, "Tensors: one-forms," Physics pages, 2011. (방문일 2011-06-25)
[다음 읽을거리]
1. 텐서 미적분학
2. 직교 좌표계 텐서 미적분학
3. 텐서를 이용한 맥스웰 방정식