[경고] 아래 글을 읽지 않고 "삼각 함수"를 보면 바보로 느껴질 수 있습니다.
1. 피타고라스의 정리
공학 문제에 빠지고 않고 등장하는 삼각 함수(trigonometric function)는 오랜 역사를 가지고 있지만 새로운 관점이 계속 발견되는 마르지 않는 샘물같은 존재이다. 함수 이름에서도 알 수 있듯이 삼각 함수는 삼각형, 특히 직각 삼각형의 비율로 정의한다. 삼각법(三角法, trigonometry)의 영어 어원은 고대 그리스어 트리고노메트론(τρίγωνομέτρον, 삼각 측량)이다. 고대 수메르와 바빌론의 천문 관측술을 전해 받은 고대 그리스인이 닮음 삼각형의 특성을 이용하여 변과 각도의 비율 관계를 발견했던 역사에서 삼각 함수의 시초를 찾을 수 있다. 기원전 300년경부여 건국 약 60년 전 기하학의 아버지 유클리드Euclid(대략 기원전 325–265)는 직각 삼각형의 특징을 체계적으로 논증했으며, 기원전 140년경위만조선 멸망 약 30년 전 삼각법의 아버지 히파르쿠스Hipparchus of Nicaea(대략 기원전 190–120)는 초보적인 삼각 함수표를 만들어 천문학에 성공적으로 응용하였다.
[그림 1]을 이용하면 사인(sine), 코사인(cosine), 탄젠트(tangent) 함수를 아래와 같이 정의할 수 있다.
 (1)
(1)
여기서 빗변(hypotenuse), 밑변(adjacent), 높이(opposite)는 각각 $h$, $b$, $a$로 표기한다.
[그림 2] 원에 있는 반현(출처: wikipedia.org)
함수
사인(sin)의 어원은 라틴어
(Latin) 시누스(sinus)이다.
접혀 있음(fold, bosom, or bay)을 뜻하는 시누스는 산스크리트어
(Sanskrit)로 활 시위
(bowstring)를 뜻하는
지바를 아라비아인이 소리나는 대로 표기하면서 문제가 시작되었다. 아라비아어
(Arabic) 입장에서 외래어인 지바는 자신들에게 없는 단어였기 때문에, 지바와 자음이 같은 접혀 있음이란 단어로 오인하여 잘못 사용되었다. 이런 실수가 수정되지 않고 유럽에도 전해져 접혀 있다는 시누스로 재번역되어 오늘날에 이르고 있다. 산스크리트어를 제대로 번역했다면, 시누스 대신 활 시위가 만드는 반현
(半弦, half the chord)에 해당하는 다른 단어가 되었어야 한다. 여기서 반현
(半弦, half the chord)은 [그림 2]에 있는
초록색 선이며 현
(弦, chord)은 [그림 4]에 있는
파란색 선이다. 이탈리아에서는 시누스에 해당하는
세노(오목함, seno)를 줄여 사인 함수를 $\operatorname{sen} x$로 표기하기도 한다. 함수
탄젠트(tan)의 어원도 라틴어
탕겐스(tangens)이다. 단어 탕겐스는
붙어있음(touching)을 의미하므로 접선
(接線, tangent)의 의미가 된다. 함수
코사인(cos)은 상보적 사인
(complementary sine) 혹은 여현
(餘弦)의 약어이며, 우리말로 더 풀어쓰면 사인을 도우는 상호 보완적인 함수가 된다. 더 정확하게 보면 코사인은 각도 측면에서 사인을 보완한다.
[직각 삼각형 관점에서 $\sin(90^\circ - \theta)$ = $\cos \theta$이므로 당연히 상보적이다. 혹은 사인과 코사인 함수값은 반지름이 1인 원을 따라 움직여야 하므로 서로 연계되어 있다.] 고등학교 수학 시간에 식 (1)을 소개하기 때문에 대부분 식 (1)의 정의는 잘 알지만, 우리는 좀더 근본적인 질문을 할 필요가 있다. 예를 들면, 직각 삼각형인 경우 삼각형의 크기에 관계없이 끼인각
[그림 1에서 $A$]이 같으면 식 (1)로 정의된 비율이 항상 같은 이유는 무엇인가? 직각 삼각형에 대해 식 (1)을 증명할 수 있을까? 닮은 삼각형은 말 그대로 서로 비슷하기 때문에 비례 관계에 의해 삼각 함수값은 일정하다고 할 수 있다. 하지만 고민을 더 깊게 해서 삼각형이 서로 닮은 경우에 식 (1)과 같은 비례가 성립하는 근본 원인을 찾아본다.
[그림 3(a)]에 있는 큰 직각 삼각형의 길이[$a_2$, $b_2$, $h_2$]가 정해진 경우, 이보다 작은 직각 삼각형[$a_1$, $b_1$, $h_1$으로 구성]을 임의로 그릴 수 있다. 이 경우 큰 직각 삼각형과 작은 직각 삼각형의 삼각비가 일정한지 증명한다.
(a) 닮은 직각 삼각형
[그림 3] 직각 삼각형의 다양한 닮은꼴
[증명: 대수 기하학]
[그림 3(a)]에서
파란색 삼각형[$a_1, b_1, h_1$으로 구성]과
분홍색 삼각형[$a_2, b_2, h_2$로 구성]은 세 각이 모두 같기 때문에 서로 닮아있다. 닮은 두 삼각형은 직각 삼각형이기 때문에
피타고라스의 정리에 의해 아래식이 성립한다.

(2)
또한, 두 삼각형의 크기는 서로 다르기 때문에 [그림 3(a)]과 같은 녹색 삼각형[$a_2-a_1$, $b_2-b_1$, $h_2-h_1$으로 구성]을 항상 만들 수 있다. 이 녹색 삼각형도 직각 삼각형이기 때문에 아래의 관계가 항상 성립한다.

(3)
여기서 식 (3)의 둘째식은 첫째식을 전개한 후 식 (2)의 피타고라스 정리를 대입하여 얻었다. 식 (3)의 마지막 결과와 식 (2)를 서로 빼주면 항등식 (4)를 얻을 수 있다.

(4)
식 (4)에 $h_1$을 곱해주면 임의의 $a_1, b_1$에 대해 성립해야 하므로 아래 사인과 코사인 함수 관계가 삼각형의 크기에 관계없이 항상 성립해야 한다.

(5)
식 (4)에서 $a_2, b_2, h_2$는 고정된 값이므로 $a_1, b_1$이 임의일 지라도 $a_1/h_1, b_1/h_1$은 변할 수 없고 고정되어야 한다.
[증명: 유클리드 기하학]
유클리드 기하학(Euclidean geometry)을 사용하면 더 직관적으로 삼각비가 일정함을 보일 수 있다. [그림 3(b)]에 있는 왼쪽 직각 삼각형처럼 빗변의 중점을 잡고 밑변과 높이에 평행한 선을 2개 그어서 작은 직각 삼각형 2개를 만들 수 있다. 그러면 두 직각 삼각형은
ASA(angle-side-angle) 합동이기 때문에 밑변과 높이가 서로 같다. 따라서 큰 직각 삼각형과 작은 직각 삼각형의 삼각비는 서로 같다. 비슷한 논리로 [그림 3(b)]의 오른쪽 직각 삼각형처럼 빗변을 등간격으로 $m$등분해서 각 점을 기준으로 밑변과 높이에 평행한 선을 긋는다. 그러면 밑변과 높이도 빗변과 같이 등간격으로 균등하게 나누어짐을 볼 수 있다. 즉, 빗변 분할로 생긴 임의의 직각 삼각형은 서로 닮아있고 변의 비율도 같다. 이로 인해 원래 직각 삼각형과 $m$등분으로 생긴 임의의 직각 삼각형의 삼각비는 항상 동일하다. 예를 들어, 빗변 길이가 $10$인 직각 삼각형과 닮은 빗변 길이가 $1.2$인 직각 삼각형을 비교해본다. 두 삼각형의 빗변 비율이 $10:1.2$ = $25:3$이므로, [그림 3(b)]의 오른쪽 삼각형처럼 길이가 $10$인 빗변을 25등분해서 균등한 길이 조각을 25개 만든다. 꼭지점부터 헤아려서 처음 3개 길이 조각이 구성하는 직각 삼각형은 빗변이 $1.2$이다. 그러면 ASA 합동에 의해 등간격으로 나눈 두 삼각형의 삼각비는 완전히 같다. 결국 직각 삼각형의 빗변을 등간격으로 나누는 과정은 매우 작은 길이까지 계속 진행될 수 있으므로, 모든 닮은 직각 삼각형의 삼각비는 항상 같다.
______________________________
위의 증명은 직각 삼각형이 아닌 임의의 삼각형으로 쉽게 확장할 수 있다. 왜냐하면 모든 임의의 삼각형은 하나 혹은 두 개의 직각 삼각형으로 생각할 수 있기 때문이다.
[∵ 점과 직선의 관계를 생각하면, 항상 점에서 직선으로 수선을 그을 수 있다.] 또한 삼각비와 같은 비례 성질은 좌표계의 특성과 밀접하게 연결되어 있다. 삼각비의 항등성과 같은
유클리드 기하학이 적용되는 데카르트 좌표계
(Cartesian coordinate system)는 모든 좌표축으로 선형의 비례 관계가 성립한다. 따라서 삼각비가 성립함은 전제하고 있는 공간이 유클리드 공간
(Euclidean space) 혹은 데카르트 좌표계라는 뜻이다. 다른 관점으로 보면, 비유클리드 공간
(non-Euclidean space)에서는 삼각비의 항등성이 데카르트 좌표계와는 전혀 다르게 구성되어야 한다. 그래서 임의 공간의 특성을 감지하는 잣대로 삼각비의 항등성은 매우 유용하다.
[그림 4] 원에 접하는 직선(출처: wikipedia.org)
위의 증명에서 항등식이 마음에 들지 않으면 아래와 같이 대수 기하학
(代數幾何學, algebraic geometry)적인 접근을 할 수 있다. 먼저 식 (2)를 $h_1^2, h_2^2$으로 나누고 $x_1, x_2$, $y_1, y_2$의 정의인 식 (6)의 첫째식을 이용해 식 (2)와 (3)을 다시 쓴다.

(6)
식 (6)의 둘째식에 의해 궤적 $(x_1, y_1)$은
반지름이 1인 원(圓, circle)의 방정식이 된다. 또한, 식 (4)처럼 $(x_2, y_2)$가 고정된 경우, 식 (6)의 셋째식이 표현하는 궤적 $(x_1, y_1)$은 원에 접하는 직선의 방정식 된다. 이를 증명하기 위해 미분 개념을 원에 적용하면 다음과 같다.


(7)
식 (7)을 보면 고정점 $(x_2, y_2)$를 지나면서 반지름이 1인 원에 접하는 접선식
[tangent equation: 그림 4에서 빨간선]이다. 따라서, 식 (6)의 둘째식과 셋째식을 동시에 만족하기 위해서는 $(x_1, y_1) = (x_2, y_2)$가 되어야 한다. 즉, 임의점 $(x_1, y_1)$은
원의 방정식[식 (6)의 둘째식]이어서 반지름이 1인 원 상의 모든 점이 될 수 있지만, 접선의 방정식
[식 (6)의 셋째식]에 의해 임의점 $(x_1, y_1)$는 고정점 $(x_2, y_2)$에 접해야 하므로 $(x_1, y_1) = (x_2, y_2)$가 된다. 따라서, 이 결과는 식 (5)와 동일하다.
[그림 5] 삼각 함수의 확장(출처: wikipedia.org)
식 (6)과 같은
원의 방정식을 이용하면 삼각 함수 개념을 [그림 5]와 같이 확장할 수 있다. 먼저 [그림 1]의 빗변을 $1$로 잡으면, 코사인과 사인 함수는 각각 직각 삼각형의 밑변과 높이에 대응한다. [그림 5]처럼 직각 삼각형을 데카르트 좌표계 상에 그리고 피타고라스의 정리
(Pythagorean theorem)를 적용한 경우, 직각 삼각형의 밑변과 높이는 원을 구성하는 좌표 성분 $x, y$가 된다. 그러면 삼각 함수는 더 이상 식 (1)과 같은 길이에 한정되지 않고 좌표계를 이용하여 식 (8)처럼 일반적으로 정의된다.
 (8)
(8)  (9)
(9)
여기서 점 $(x, y)$는 식 (6)과 같이 반지름이 1인 원[$x^2 + y^2 = 1$] 위에 있고, $\sec \theta$, $\csc \theta$, $\cot \theta$는 각각 시컨트(secant), 코시컨트(cosecant), 코탄젠트(cotangent) 함수라 부른다. [그림 5]를 통해 사인과 코사인 함수의 주기(週期, period: 값이 반복되는 범위)는 $2 \pi$[= $360^\circ$], 탄젠트 함수의 주기는 $\pi$[= $180^\circ$]가 됨을 쉽게 알 수 있다.[∵ 그림 5에서 사인 함수는 $y$축값, 코사인 함수는 $x$축값, 탄젠트 함수는 직선의 기울기이므로]
식 (8)과 (9)의 개념을 이용하면 다양한 삼각 함수 공식을 쉽게 증명할 수 있다.

(10)

(11)
[그림 6] 법선을 가진 삼각형(출처: wikipedia.org)
[사인 법칙(law of sines)]
 (12)
(12)
[그림 6]과 같은 법선(法線, normal)을 가진 삼각형을 고려하면 아래 관계식이 항상 성립한다.

(13)
______________________________
[코사인 제1 법칙(the first law of cosines)]
 (14)
(14)
[그림 6]의 삼각형과 법선을 고려하면 식 (14)가 쉽게 증명된다.
______________________________
[코사인 제2 법칙(the second law of cosines)]
 (15)
(15)
식 (14)의 위쪽 두 개 식에 $a, b$를 각각 곱하면 다음을 얻을 수 있다.

(16)
식 (14)의 셋째식에 $c$를 곱한 후 식 (16)을 대입하면 식 (15)가 증명된다.

(17)
______________________________
[탄젠트 법칙(law of tangents)]
 (18)
(18)
[증명]
식 (12)에 제시한 사인 법칙을 적용하면 변과 각은 다음 관계를 가진다.
 (19)
(19)
식 (19)에
삼각 함수의 합차 공식을 적용하면 식 (18)이 증명된다.
______________________________
식 (9)에 있는 함수 시컨트
(sec)는 어원이 라틴어 세칸스
(secans)이다. 단어 세칸스는
자르기(cutting)를 의미한다. 우리말로는 할선
(割線, secant)이라 한다. 그런데 시컨트를 정의하기 위해 원에서 어느 부분을 자를까? 이를 이해하기 위해 [그림 7]을 세심하게 본다.
[그림 7] 원으로 정의한 삼각 함수(출처: wikipedia.org)
시컨트 함수는 원에 접선인 탄젠트 함수가 $x$축과 만나는 점까지의 길이이다. 이 관계는 식 (6)에 있는 접선의 방정식을 식 (20)처럼 쓰면 명확히 보인다.

(20)
또한 식 (11)의 관계식으로 인해 함수 시컨트(sec), 탄젠트(tan)는 직각 삼각형을 [그림 7]과 같이 이룬다. 따라서 [그림 7]을 다시 보면, 시컨트는 원을 뚫고 나오고 있다. 즉, 자르는 선인 할선이 된다.
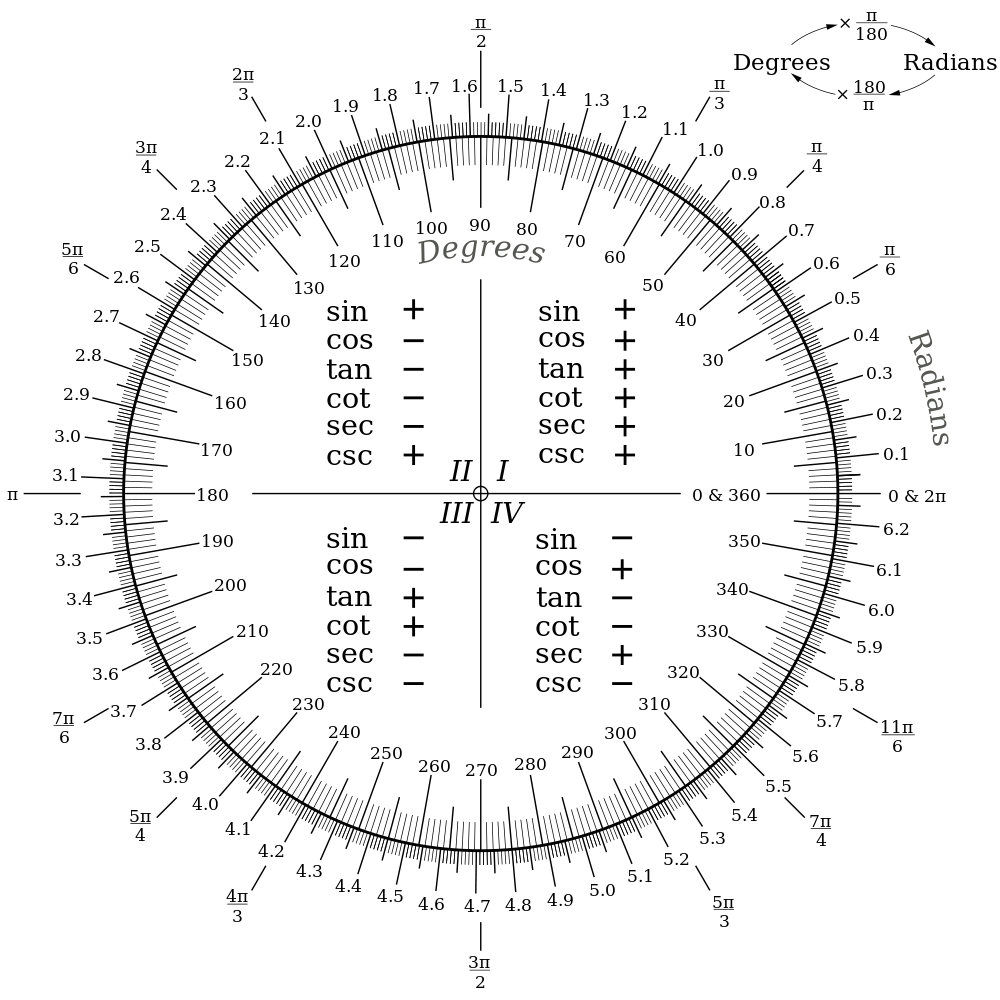
[그림 8] 라디안의 개념(출처: wikipedia.org)
삼각 함수에서 빠질 수 없는 개념은 [그림 8]로 정의하는
라디안(radian)이다. 라디안을 이용한 각도 표현법은 호도법
(弧度法, circular measure)이라 한다. 또한 라디안은
빛줄기(ray or beam)를 뜻하는 라틴어 라디우스
(radius)에 뿌리를 두고 있고, 라디안의 끝에 있는 접미사 안
(-an)은 도구를 뜻한다. 그래서 라디안을 순우리말로 직역하면
빛개가 된다. 라디안 개념을 바탕으로 각도 $\theta$를 표현하면 다음과 같다.

(21)
여기서 $l$은 호의 길이(arc length), $r$은 반지름(radius), $\theta$는 라디안으로 정의한 각도, $\vartheta$는 360˚ 기준 각도이다. 식 (21)의 우변 식은 라디안 $\theta$를 360˚ 기준 $\vartheta$로 바꾸기를 의미한다. 예를 들어, $\theta = \pi$ rad를 대입하면 $\vartheta = 180/\pi \cdot \pi = 180^\circ$를 얻을 수 있다. 자세한 라디안과 각도 관계는 [표 1]을 참고한다.
[표 1] 라디안(radian)과 도(degree)로 표현한 각도 관계식
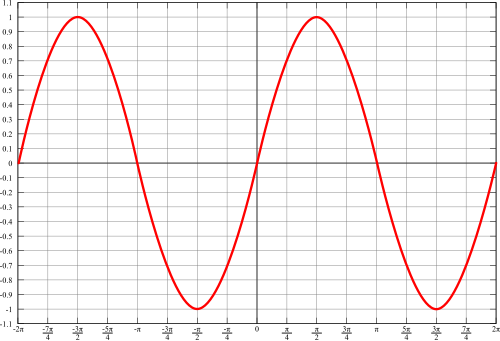
[그림 9] 사인 함수의 모양(출처: wikipedia.org)
삼각 함수의 입력값은 위상(位相, phase)이라 부른다. 위상을 쉽게 표현하면 현재 위치의 모양[혹은 양상]이란 의미다. [그림 9]의 삼각 함수처럼 특정 모양이 주기적으로 반복되는 함수는 주기 함수(periodic function)라 부른다.
 (22)
(22)
여기서 $T$는 주기이다. 사인이나 코사인 함수의 주기는 $2 \pi$[= 360˚], 탄젠트 함수는 $\pi$[= 180˚]이다. 사실 위상은 주기 함수의 주기성 혹은 반복 특성 때문에 사용한다. 이 반복되는 모양에서 특정한 $x$축 위치를 제대로 가리키기 위해 위상을 쓴다. 그러면 같은 모양이 반복되더라도 $x$축의 특정 위치를 정확히 선택할 수 있다.
그런데 편리한 각도 개념을 두고 왜 라디안을 사용할까? 이 개념을 이해하려면
삼각 함수의 미분을 공부해야 한다. 라디안으로 정의하면 삼각 함수의 미분이 식 (23)처럼 매우 간단해진다.
여기서 $\sec x$ = $1 \mathbin{/} \cos x$, $\csc x$ = $1 \mathbin{/} \sin x$, $\cot x$ = $\cos x \mathbin{/} \sin x$이다.
[그림 10] 사인 및 코사인 역함수의 모습(출처: wikipedia.org)
[그림 11] 시컨트 및 코시컨트 역함수의 모습(출처: wikipedia.org)
[그림 12] 탄젠트 및 코탄젠트 역함수의 모습(출처: wikipedia.org)
[표 1] 역삼각 함수의 정의역과 치역
| 역삼각 함수 | 정의역 | 치역의 주치 |
|---|
| $\sin^{-1} x$ | $-1 \le x \le 1$ | $-\pi/2 \le y \le \pi/2$ |
| $\cos^{-1} x$ | $-1 \le x \le 1$ | $0 \le y \le \pi$ |
| $\sec^{-1} x$ | $x \le -1$ 혹은 $x \ge 1$ | $0 \le y < \pi/2$ 혹은 $\pi/2 < y \le \pi$ |
| $\csc^{-1} x$ | $x \le -1$ 혹은 $x \ge 1$ | $-\pi/2 \le y < 0$ 혹은 $0 < y \le \pi/2$ |
| $\tan^{-1} x$ | 모든 실수 | $-\pi/2 < y < \pi/2$ |
| $\cot^{-1} x$ | 모든 실수 | $0 < y < \pi$ |
삼각 함수는 주기 함수라서 역함수를 정의하기는 불가능하다. 하지만 워낙 삼각 함수가 많이 쓰이므로, 삼각 함수의 정의역을 제한해서 삼각 함수의 $x, y$를 일대일 대응시킨다. 그러면 제한된 영역에 한해서 삼각 함수는 역함수를 가지고, 이를 역삼각 함수(inverse trigonometric function)라 명한다. 역함수가 존재하는 범위를 통상적으로 역삼각 함수의 주치(主値, principal value)라 부른다. 역삼각 함수 중에서 탄젠트와 코탄젠트 역함수는 주치의 범위가 $\pi$밖에 되지 않아 조금 불만이다. 그래서 함수 입력을 단일 변수가 아닌 2차원 $xy$-평면 전체로 만들어서 주치의 범위를 $2 \pi$로 확장한 2변수 탄젠트 역함수(2-variable arctangent function) $\operatorname{atan2}(y, x)$가 빈번하게 쓰인다. 여기서 $x$ = $\rho \cos \theta$, $y$ = $\rho \sin \theta$, $\rho$는 반지름이다. 2변수 탄젠트 역함수는 $x, y$의 부호를 모두 고려함으로써 주치를 $(-\pi, \pi]$로 만들어서 주치의 범위를 $\tan^{-1} x$보다 2배 키운다. 상대적으로 2변수 코탄젠트 역함수(2-variable arccotangent function) $\operatorname{acot2}(x, y)$는 잘 쓰이지 않지만 정의는 가능하다. 2변수 코탄젠트 역함수의 주치는 보통 $(-\pi/2, 3\pi/2]$로 선택한다. 역삼각 함수의 주치를 도입해서 미분도 편리하게 정의한다.
여기서 증명에는
역함수의 미분 공식을 사용, 미분 부호는 주치 혹은 [그림 10–12]로 선택한다.
 (1)
(1) (2)
(2) (3)
(3)
 (4)
(4) (5)
(5) (6)
(6)
 (7)
(7) (8)
(8) (9)
(9) (10)
(10) (11)
(11) (12)
(12) (13)
(13) (14)
(14) (15)
(15) (16)
(16)




 (2)
(2) (3)
(3) (4)
(4) (5)
(5)
 (6)
(6)
 (7)
(7)



 (10)
(10) (11)
(11)

 (13)
(13)

 (16)
(16) (17)
(17)


 (20)
(20)




 (23c)
(23c)


 (24a)
(24a) (24b)
(24b) (24c)
(24c)