구심력과 원심력(Centripetal and Centrifugal Forces)

[경고] 아래 글을 읽지 않고 "구심력과 원심력"을 보면 바보로 느껴질 수 있습니다.
1. 미분법의 의미
2. 뉴턴의 운동 법칙

[그림 1] 구심력의 정의(출처: wikipedia.org)

[그림 1]과 같은 운동체가 회전 운동을 하기 위해서는 반드시 구심력(求心力, centripetal force)이라는 안으로 잡아당기는 힘이 필요하다. 구심력의 크기를 구하기 위해 데카르트 좌표계(Cartesian coordinate system) 상에서 회전 운동을 기술해보자.

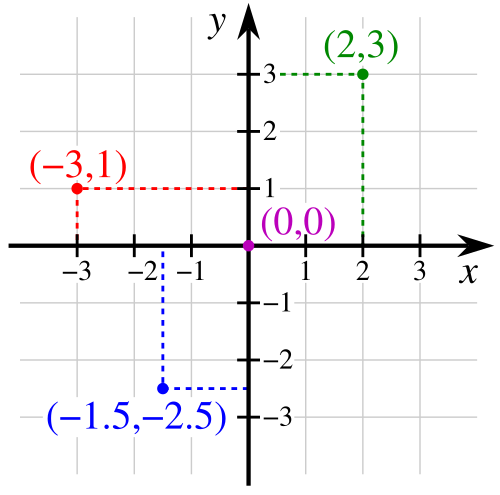
[그림 2] 2차원과 3차원 데카르트 좌표계(출처: wikipedia.org)

운동체는 [그림 1]과 같이 일정한 각주파수(angular frequency) $\omega$로 원 운동을 하므로, 특정 시간 $t$에서의 위치(displacement) $(x, y)$, 속도(velocity) $v$, 가속도(acceleration) $a$는 아래처럼 쓸 수 있다.

                       (1)

식 (1)을 이용하여 식 (2)의 뉴턴의 운동 법칙(Newton's law of motion)을 다시 쓰면 아래와 같다.

                       (2)

                       (3)

구심력 공식인 식 (3)은 뉴턴의 운동 법칙으로 보통 증명하지만, 최초 제안자는 네델란드의 만물박사인 하위헌스Christiaan Huygens(1629–1695)이다. 하위헌스는 뉴턴 이전인 1659년하위헌스 30세, 조선 효종 시절에 기하학적 논증만으로 식 (3)을 유도했다. 식 (3)에서 얻은 구심력을 [그림 3]과 같은 위치 벡터(position vector: 원점에서 좌표점으로 가는 벡터) 관점에서 바라보자.

[그림 3] 위치 벡터의 표현(출처: wikipedia.org)

식 (3)에 의해 구심력은 위치 벡터의 반대 방향이므로[∵ 위치 벡터는 원점을 뚫고 밖으로 나가는 벡터이므로] [그림 1]과 같이 원 운동의 중심으로 향하는 힘이 된다. 구심력을 에너지(energy) 관점으로 보면, 실제적인 일(work)이 없다. 왜냐하면 구심력이 작용하는 방향과 운동체가 움직이는 방향이 항상 수직이기 때문이다.

[원심 분리기(centrifuge)의 동작 원리]

원심력(遠心力, centrifugal force)은 구심력이 있기 때문에 존재할 수 있는 가상의 힘(fictitious force)이다. 즉, [그림 1]과 같이 회전 운동하는 운동체 내부에 있는 관찰자가 느끼는 가상의 힘을 원심력이라 한다. 예를 들면 자동차가 회전할 때 승객이 느끼는 바깥으로 밀려나는 듯한 힘이 바로 원심력이다. 승객이 자동차에 완전 결합되어 있으면 원심력을 느끼지 못하겠지만, 승객과 자동차의 연결은 느슨하기 때문에 자동차는 정상적으로 구심력[혹은 바퀴의 마찰력]에 의해 회전하나 승객은 관성에 의해 바깥으로 밀려나게 된다. 왜냐하면 자동차는 구심력에 의해 중심으로 당겨지나 승객은 관성에 의해 중심의 반대 방향으로 밀려나는 듯한 느낌을 받기 때문이다.

[다음 읽을거리]
1. 최초의 입자 가속기 사이클로트론