[경고] 아래 글을 읽지 않고 "행렬의 반복법"을 보면 바보로 느껴질 수 있습니다.
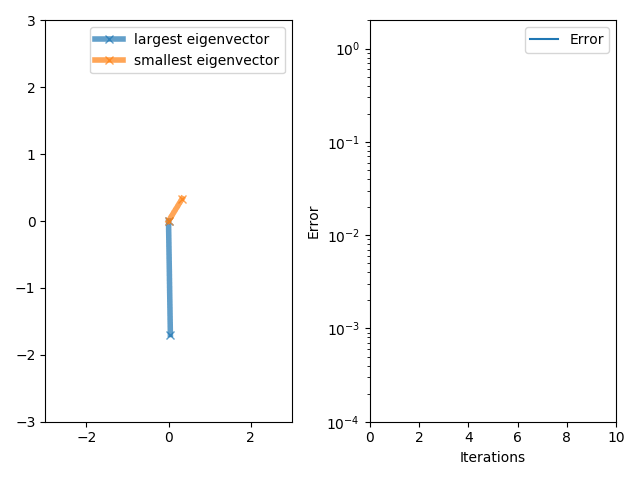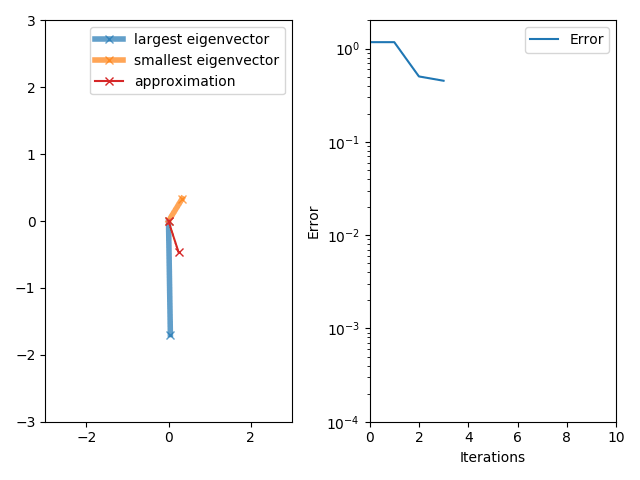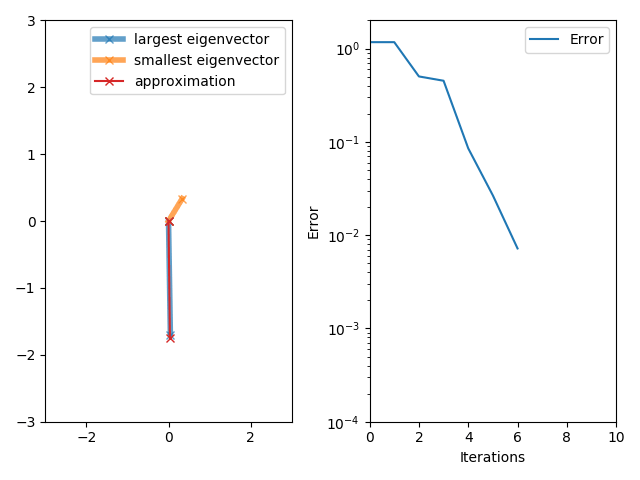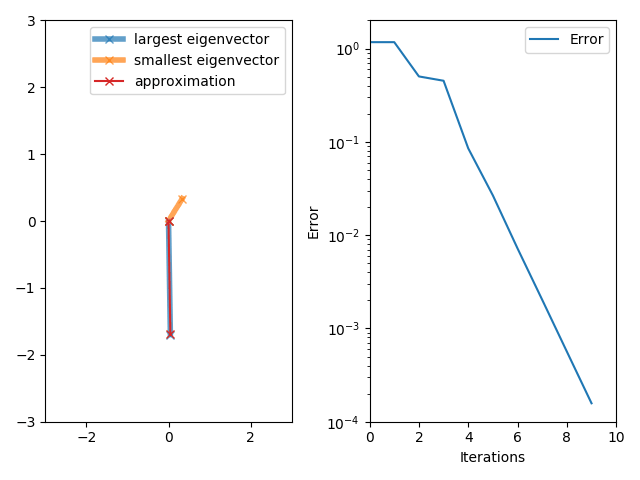
[그림 1] 고유 벡터를 구하기 위한 반복법(출처: wikipedia.org)
행렬(matrix) 이론은 잘 개발되어 있기 때문에 원하는 답을 언제나 정확하게 얻을 수 있다. 하지만 행렬의 차원이 커지면 계산 시간이 매우 빠르게 증가해서, 행렬 알고리즘(matrix algorithm or algorism)은 있으나 없는 것과 마찬가지인 상황이 빈번하게 생긴다. 그래서 매우 큰 행렬을 연산할 때는 정확함보다는 주어진 시간에 근사해를 얻는 방법이 필요하다. 행렬은 현실 문제를 푸는 합리적인 방법론이라서, 큰 차원의 행렬을 연산하기 위한 효율적인 반복법(iterative method)이 잘 발달되어 있다.
반복법으로 역행렬(inverse matrix)을 간단히 계산할 수 있. 원칙적으로 역행렬은 가우스–요르단 소거법(Gauss–Jordan elimination)으로 정확히 계산하지만, 행렬의 차원이 커지면 어마어마한 계산 시간으로 인해 반복법을 쓸 수밖에 없다. 역행렬의 반복법을 위해 행렬 $\bf T$에 대한 부분 합 ${\bf S}_m$을 구한다.
 (1)
(1)만약 $m$이 커질 때 ${\bf T}^m$이 $0$으로 간다면, 식 (1)을 이용해 역행렬을 다음처럼 표현할 수 있다.
 (2)
(2)따라서 어떤 행렬 $\bf A$의 역행렬은 식 (2)에 ${\bf T}$ = ${\bf I} - {\bf A}$를 대입해 계산할 수 있다. 식 (2)와 같은 방법을 쓰면, 다양한 역연산(inverse operator)을 무한 급수(infinite series)로 정의할 수 있다. 이 경우, 식 (2)에 나타나는 무한 급수를 노이만 급수(Neumann series)라 한다. 노이만 급수는 1877년노이만 45세, 조선 고종 시절에 노이만Carl Neumann(1832–1925)이 제안하였다. 이외에도 노이만은 노이만 경계 조건(Neumann boundary condition)으로도 유명하다. 노이만의 아버지Franz Ernst Neumann(1798–1895)는 자기장(magnetic field)에 나오는 자기 벡터 포텐셜(magnetic vector potential)과 노이만 공식(Neumann formula)을 제안하였다.
식 (2)에 등장한 노이만 급수의 수렴성을 판정한다. 임의의 열 벡터 $\bf x$를 곱해도 식 (2)의 우변에 있는 무한 급수는 수렴한다고 가정한다. 이 조건을 이용해 열 벡터 $\bf x$를 $n$개의 고유 벡터(eigenvector) ${\bf x}_i$에 대한 선형 결합으로 바꾸어서 노이만 급수에 곱한다.
 (3)
(3)여기서 $\lambda_i$는 고유 벡터 ${\bf x}_i$에 대한 고유값(eigenvalue), $\bf T$의 차원은 $n \times n$이다. 식 (3)의 마지막식이 모든 경우에 수렴하려면, 최대 고유값의 크기가 $1$보다 작아야 한다. 따라서 노이만 급수의 수렴 조건은 행렬 $\bf T$에 대해 $\Lambda_\text{max} < 1$이다. 여기서 $\Lambda_\text{max}$는 크기가 가장 큰 고유값[= $\max(|\lambda_i|)$]을 의미한다.
보통 가우스 소거법(Gaussian elimination)으로 푸는 연립 일차 방정식 ${\bf Ax}$ = $\bf b$도 반복법으로 해결할 수 있다. 행렬 $\bf A$를 나누어서 $\bf A$ = ${\bf S} - {\bf T}$라고 둔다. 그러면 연립 일차 방정식의 해인 열 벡터 $\bf x$를 다음과 같은 반복법으로 표현할 수 있다[1].
 (4)
(4)여기서 $k$가 커지면 ${\bf x}_k$는 $\bf x$에 수렴한다고 가정한다. 식 (4)의 왼쪽과 오른쪽 등식을 서로 빼서 반복법의 오차 벡터 ${\bf e}_k$에 대한 관계식을 만든다.
 (5)
(5)여기서 ${\bf e}_k$ = ${\bf x} - {\bf x}_k$이다. 다음 단계로 식 (3)에 있는 위쪽 등식처럼 오차 벡터를 고유 벡터의 선형 결합으로 바꾼다.
 (6)
(6)여기서 $\lambda_i$는 ${\bf S}^{-1}{\bf T}$의 제$i$번째 고유값, ${\bf S}^{-1}{\bf T}$의 차원은 $n \times n$이다. 따라서 모든 고유값이 $|\lambda_i| < 1$을 만족하면, 식 (4)에서 얻은 반복법의 결과는 해 $\bf x$에 수렴한다. 혹은 더 쉽게 크기가 가장 큰 $\Lambda_\text{max}$가 $1$보다 작으면 반복법은 수렴한다. 또한 반복법의 수렴 속도는 최대 크기의 고유값 $\Lambda_\text{max}$에 달려있다. 그래서 로랑 급수(Laurent series)의 수렴 반경(radius of convergence)처럼 $\Lambda_\text{max}$를 스펙트럼 반경(spectral radius)이라 부른다.
 (7)
(7)수렴 조건을 표현할 때, 주파수 범위를 뜻하는 스펙트럼이 쓰여서 약간 이상하다. 하지만 주파수에 대한 푸리에 급수(Fourier series)처럼 고유 벡터를 이용해 임의의 열 벡터를 분해한 후 반복법의 수렴 특성을 분석하므로, 스펙트럼 반경은 나름 타당한 용어이다. 또한, 스펙트럼 반경은 노이만 급수의 항이 무한대로 갈 때의 점근적 수렴성을 나타내는 특성으로 인해 점근 수렴 인자(asymptotic convergence factor)라고 부르기도 한다.
식 (4)에 기반한 반복법을 사용하려면, $\bf S$의 역행렬을 구해야 한다. 큰 행렬의 역행렬은 또 다른 문제점을 만들기 때문에, $\bf S$의 선택은 반복법의 효율에 결정적인 영향을 끼친다. 그래서 효율적으로 $\bf S$의 역행렬을 구하기 위해, $\bf S$는 보통 대각 행렬(diagonal matrix)이나 삼각 행렬(triangular matrix)로 택한다. 이로 인해 $\bf S$를 반복법을 위한 전조건자(preconditioner)라 부른다. 행렬 $\bf S$를 대각 행렬로 간편하게 선택하는 반복법은 야코비 방법(Jacobi method)이라 한다. 야코비 방법을 쓰기 위해 ${\bf A}, {\bf S}, {\bf T}$를 다음과 같이 정한다.
 (8a)
(8a) (8b)
(8b)식 (8)을 식 (4)에 대입해서 정리하면, 야코비 방법의 반복 공식을 얻는다.
 (9a)
(9a) (9b)
(9b)여기서 $\bf S$ = $\bf D$, $\bf T$ = $-({\bf L} + {\bf U})$, $\bf A$ = ${\bf S} - {\bf T}$ = ${\bf D}+{\bf L}+{\bf U}$, 그리고 ${\bf D}, {\bf L}, {\bf U}$는 각각 대각, 하삼각, 상삼각 행렬(diagonal, and lower and upper triangular matrices)이다. 다음처럼 $\bf S$를 하삼각 행렬(lower triangular matrix)로 선택한 반복법은 가우스–자이델 방법(Gauss–Seidel method)이 된다.
 (10)
(10)식 (10)을 식 (4)에 넣어서 $x_i^{(k+1)}$을 중심으로 모으면 가우스–자이델 방법을 위한 공식이 만들어진다.
 (11a)
(11a) (11b)
(11b)여기서 $\bf S$ = ${\bf D} + {\bf L}$, $\bf T$ = $-{\bf U}$, $\bf A$ = ${\bf S} - {\bf T}$ = ${\bf D}+{\bf L}+{\bf U}$이다. 야코비 방법과 가우스–자이델 방법을 가중치 $\omega$로 합쳐서 수렴 속도가 빠른 새로운 반복법을 만들 수 있다. 이 반복법은 축차 가속 완화(逐次加速緩和, successive over-relaxation, SOR) 방법 혹은 SOR 방법이라 부른다[5]. 축차는 다음 순서라는 뜻이며, 축차 가속은 다음 순서에도 동일한 완화값을 써서 반복법이 가속된다는 의미이다. 수학에서 완화(緩和, relaxation)는 엄격하지 않은 느슨한(relax) 방법으로 답을 찾는 전략, 혹은 풀기 쉬운 문제로 바꾸어서 답을 대충 근사하는 방식을 뜻한다. 완화를 계속 반복하면 대부분 답에 수렴하지만, 발산할 수도 있어서 완화를 적용할 때는 수렴성을 꼭 확인해야 한다. 최적화(optimization) 기법 중에서 공간 사상(space mapping)은 완화에 기반을 두고 있다.

[그림 2] 완화 인자 $\omega$ 변화에 대한 스펙트럼 반경 $\rho$의 특성(출처: wikipedia.org)
먼저 SOR 방법을 적용하기 위해 행렬 $\bf A$를 다음처럼 $\bf A$ = ${\bf D} + {\bf L} + {\bf U}$로 나눈다.
 (12)
(12)여기서 $\bf D$ = $\operatorname{diag}(a_{11}, a_{22}, \cdots, a_{nn})$, ${\bf L}$과 ${\bf U}$는 LU 분해와 전혀 관계없이 $\bf A$의 좌하단 및 우상단 원소로 각각 구성한다. 식 (12)에 나온 ${\bf L}$과 ${\bf U}$는 각각 엄격 하삼각 및 상삼각 행렬(strictly lower and upper triangular matrices)이 된다. SOR 방법은 하삼각 행렬을 쓰는 가우스–자이델 방법이 중심이며, 가중치 $\omega$를 가우스–자이델 방법에 곱한다. 추가적으로 $x_i^{(k+1)}$을 구할 때, 야코비 방법적 요소를 추가하기 위해 대각 행렬에 가중치 $1-\omega$를 곱해 $x_i^{(k+1)} - x_i^{(k)}$를 수정 항으로 사용한다.
 (13)
(13)여기서 가중치 $\omega$는 완화 인자(relaxation factor)라 부른다. 완화 인자 $\omega$가 $1$이면, SOR 방법은 가우스–자이델 방법과 동일하다. 완화 인자가 $\omega < 1$ 및 $\omega > 1$인 값을 가지는 경우는 각각 감속 완화(減速緩和, under-relaxation)와 가속 완화(加速緩和, over-relaxation)라 이름 붙인다[6]. 완화 인자 $\omega$는 보통 $0 < \omega < 2$ 사이에서 있으며,[과감하게 $\omega$를 복소수로 확장하기도 한다.] 통상적으로 [그림 2]처럼 $1 < \omega < 2$의 범위에서 스펙트럼 반경이 최소가 되도록 $\omega$ = $\omega_\text{opt}$를 선택한다. 여기서 $\omega_\text{opt}$는 최적 완화 인자(optimal relaxation factor)이다. 식 (13)을 $x_i^{(k+1)}$에 대한 공식으로 표현하면 다음과 같다.
 (14)
(14)식 (13), (14)에서 $\omega$가 $0$ 가까이 갈 때의 성질은 무엇일까? 우리가 원하는 해답을 찾기 위해 노이만 급수인 식 (2)를 식 (13)에 적용해서 정리한다.
 (15)
(15)우세 항 $\omega$만 남기고 고차 항을 모두 없애서 더욱 간략화한다.
 (16)
(16)반복을 통해서 식 (16)이 수렴하게 되는 해는 야코비 방법에 의한 식 (9)가 된다.
 (17)
(17)따라서 $\omega \to 0$으로 간 경우에 SOR 방법은 야코비 방법에 수렴한다.
[참고문헌]
[1] G. Strang, Linear Algebra and its Applications, 4th ed., Brooks/Cole, 2006.
[2] D. M. Young, Iterative Solution of Large Linear Systems, New York: Dover Publications, 1971.
[3] R. S. Varga, Matrix Iterative Analysis, 2nd ed., Berlin: Springer-Verlag, 1991.
[4] W. Auzinger and J. M. Melenk, Iterative Solution of Large Linear Systems, 2017. (방문일 2020-09-04)
[5] D. M. Young, Iterative Methods for Solving Partial Difference Equations of Elliptic Type, Ph.D. Thesis, Harvard University, 1950. (방문일 2020-09-04)
[6] P. Wild and W. Niethammer, "Over and underrelaxation for linear systems with weakly cyclic Jacobi matrices of index $p$," Linear Algebra Appl., vol. 91, pp. 29–52, Jun. 1987.
[7] A. Hadjidimos, "Successive overrelaxation (SOR) and related methods," J. Comput. Appl. Math., vol. 123, no. 1–2, pp. 177–199, Nov. 2000.
댓글 없음 :
댓글 쓰기
욕설이나 스팸글은 삭제될 수 있습니다. [전파거북이]는 선플운동의 아름다운 인터넷을 지지합니다.