조금은 느리게 살자: 11월 2010

[경고] 아래 글을 읽지 않고 "조화 급수와 오일러–마스케로니 상수"를 보면 바보로 느껴질 수 있습니다.
1. 무한 급수
2. 테일러 급수
3. 이항 정리

조화 급수(調和級數, harmonic series)는 아래처럼 표현되는 급수이다.

(1)

이름에서도 알 수 있듯이 조화 급수는 음악과 밀접한 연관을 가지고 있다.

[그림 1] 고조파의 생성 모습(출처: wikipedia.org)

[그림 1]과 같이 현악기에 힘을 가하면 고조파(高調波, harmonics)가 생성된다. 이 고조파는 우리가 듣기에 아름다운 소리이다. 고조파를 물리적으로 표현하면 기본 주파수(fundamental frequency)의 정수배가 되는 주파수이다. 이를 파장 관점으로 쓰면 [그림 1]과 같이 분수로 표현되는 관계를 얻을 수 있다. [그림 1]처럼 기본 주파수의 분수로 표현되는 모두 모은 수를 조화 급수로 정의한다.

조화 급수에서 더하는 항의 수를 무한대로 가져가면 어떻게 될까? $N \to \infty$로 가더라도 수열은 $1/N \to 0$에 수렴하므로 무한 급수(infinite series)는 수렴할 수도 있다. 하지만 결과는 극적이다. 우리 상식과는 다르게 아래의 무한 급수는 놀랍도록 느리게 발산한다.

(2)

식 (2)가 발산함은 여러 가지 방법으로 증명할 수 있다.

[증명: 비교 판정(comparison test)]

무한 급수의 수렴 판정법 중에서 비교 판정을 이용하면 손쉽게 식 (2)가 발산함을 증명할 수 있다.

(3)
______________________________

위의 증명법은 이미 오렘Nicole Oresme(1325–1382) 주교가 1350년대오렘 25세 무렵, 고려 공민왕 시절에, 지금으로부터 약 700년전에 제시하였다. 참 놀랄만한 일이지만, 기본 출발점은 매우 간단하다. 자연수 $n+1$과 $2n$ 사이에는 $n$개의 자연수가 있고, 이를 역수해서 합산한 값은 $n/(2n)$ = $1/2$보다 항상 크다. 따라서 이러한 묶음은 무한히 있기 때문에 조화 급수는 반드시 발산한다.

[증명: 발산 급수의 성질]

식 (2)의 무한 급수를 아래와 같이 분해해 보자.

(4)

식 (4)의 최종식을 보면 처음 시작한 식과 동일하다. 하지만 부등호가 있으므로 서로 같을 수 없고 서로 달라야 한다. 결국 식 (4)는 발산해야 논리가 맞다.

______________________________

발산 수열에는 식 (4)와 같이 우리 상식으로는 이해할 수 없는 성질이 출현한다. 여기서 우리가 기억할 부분은 무한대는 수가 아니고 값이 증가해가는 상태임이다. 수렴하지 않고 끝없이 증가하기 때문에 식 (4)와 같은 기묘한 특성이 얻어진다.

식 (4)를 수학적으로 생각해보자. 식 (4)가 성립하면 해당 수열은 절대 수렴하지 않는다. 절대 수렴하지 않으므로 당연히 유계도 되지 않는다. 하지만, 조화 급수는 양수를 계속 더하고 있으므로 단조 증가하고 있다. 즉, 단조 증가하면서 유계가 되지 않으므로 필연적으로 발산해야 한다.

[증명: 이항 정리]

재미있는 이항 정리(binomial theorem)를 아래처럼 고려하자.

(5)

식 (5)는 이항 정리의 성질에 의해 $|x| < 1$인 경우에만 성립한다. 다시 식 (5)를 적분해 보자.

(6a)

(6b)

여기서 $\log(x)$는 자연 로그(natural logarithm)이다. 식 (6)에 대해 $x \to 1$로 가는 극한을 취하자. 그러면 식 (6)의 우변은 식 (2)가 되고 식 (6)의 좌변은 무한대로 발산한다. 따라서, 식 (2)는 발산한다.

______________________________

자연 로그가 나오는 식 (6)과 같은 무한 급수는 발견자 이름을 따서 뉴턴–메르카토르 급수(Newton–Mercator series)라 명한다. 뉴턴Isaac Newton(1643–1727)과 독립적으로 1668년메르카토르 48세, 조선 현종 시절에 이 급수를 발표한 메르카토르Nicholas Mercator(1620–1687)는 지도 제작에 쓰이는 메르카토르 투영(Mercator projection)을 만든 메르카토르Gerardus Mercator(1512–1594)와는 동명이인이다. 급수 발견자답게 메르카토르는 자신의 책에 자연 로그라는 명칭을 처음 사용했다.

수렴에 대한 고찰이 없었어도 무한 급수(infinite series)를 오류 없이 자유자재로 썼던 오일러Leonhard Euler(1707–1783)의 원초적인 증명도 살펴본다.

[오일러의 증명]

식 (5)에 있는 이항 정리를 이용하면 아래가 성립한다.

(7)
______________________________

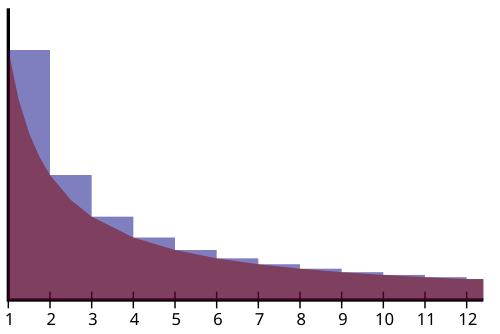
[그림 2] 오일러–마스케로니 상수의 의미(출처: wikipedia.org)

식 (6)의 결과로 인해 조화 급수의 발산값은 점근적으로 로그 함수(logarithm function)의 특성을 따른다. 식 (8)을 보면 분명하다.

(8)

식 (6)과 (8)을 이용하여 오일러–마스케로니 상수(Euler-Mascheroni constant)를 아래와 같이 정의할 수 있다.

(9)

오일러–마스케로니 상수의 의미는 [그림 2]에서 드러난다. 파란색의 높이는 조화 급수의 항($1/n$)을 나타내고 보라색은 함수 $1/x$(이 함수의 면적이 로그 함수)를 표현한다. 이 둘의 차이인 파란색의 합이 오일러–마스케로니 상수가 된다. 오일러–마스케로니 상수를 그리스 문자 $\gamma$(감마, gamma)로 쓰는 이유는 이 상수가 감마 함수(gamma function)의 미분과 밀접한 관계를 가지기 때문이다. 식 (9)로 정의된 오일러–마스케로니 상수 $\gamma$를 어림해 보자. 먼저 로그 함수의 미분 공식을 이용하여 정적분을 계산하자.

(10)

정적분의 특성에 의해 식 (10)으로 표현된 적분은 아래와 같은 한계를 가진다. 쉽게 생각하려면 [그림 2]를 참고하자.

(11)

식 (11)의 부등식은 $1/x$ 함수가 단조 감소한다는 성질을 이용하면 쉽게 얻을 수 있다. 식 (11)을 식 (1)의 조화 급수 관점에서 쓰고 정리하면 아래를 얻을 수 있다.

(12)

식 (12)의 증명처럼 모든 $n$에 대해 $H_n - \log n$은 항상 양수이다. 즉, 조화 급수는 로그 함수보다 항상 크다. 하지만 그 차이는 1보다는 작은 범위에 있다. 다음으로 $n \to \infty$로 가는 극한을 취하면 오일러–마스케로니 상수 $\gamma$의 한계를 얻을 수 있다.

(13)

이 상수가 수렴함을 최종적으로 증명하려면 $H_n - \log n$이 단조 증가하거나 단조 감소해야 한다. 증감 특성을 얻기 위해 아래 식을 고려하자.

(14)

식 (14)로부터 $H_n - \log n$은 $n$이 커짐에 따라 단조 감소한다. 따라서 오일러–마스케로니 상수 $\gamma$는 유계이며 단조 감소하므로 수렴한다. 오일러–마스케로니 상수의 정확한 값은 아래와 같다[1].

$\gamma$ = 0.57721566490153286060651209008240243104215933593992...

조화 급수와 로그 함수로 정의할 수 있는 쉬워 보이는 상수인 $\gamma$는 절대 만만하지 않다. 예를 들어, 현재까지 $\gamma$가 무리수인지 유리수인지 증명되지 않고 있다. 딱 봐도 $\gamma$는 무리수처럼 보이지만, 증명하지 못하면 단정할 수 없고 모른다고 해야 한다.

오일러–마스케로니 상수는 아래와 같은 다양한 방식으로 정의해서 사용할 수 있다.

1. 상수 표현식(constanst representation)

[베르누이 수(Bernoulli number)]

(1.1)

여기서 $B_m$은 제$m$번 베르누이 수(Bernoulli number)이다.

[증명]

무한 급수 계산에 매우 유용한 오일러–매클로린 공식(Euler–Maclaurin formula)에서 시작하자. 식 (10)에 기반하여 $f(x) = 1/x$라 놓고 오일러–매클로린 공식을 적용하면 다음과 같다.

(1.2)

다음으로 함수 $f(x)$의 $m$번 미분식을 구한다.

(1.3)

식 (1.3)을 식 (1.2)에 대입해서 오일러–마스케로니 상수 형태로 만든다.

(1.4)

식 (1.4)에서 $n$을 무한대로 보내면 식 (1.1)을 얻을 수 있다.

______________________________

식 (1.1)을 실제 계산에 적용할 때는 주의할 점이 있다. 지표 $m$이 커지면 베르누이 수는 발산하기 때문에, 식 (1.1)에 있는 무한 급수의 부분 합은 수렴하지 않고 진동하면서 발산한다. 따라서 식 (1.1)의 우변은 수렴하지 않으므로 오일러–마스케로니 상수에 대한 적절한 표현식이 아니다. 이로 인해 식 (1.1)은 무한 급수 대신 적절한 유한 합을 이용해 계산한다. 예를 들어 다음처럼 오일러–마스케로니 상수를 어림할 수 있다.

(1.5)