전압파와 전류파(Voltage and Current Waves)

[경고] 아래 글을 읽지 않고 "전압파와 전류파"를 보면 바보로 느껴질 수 있습니다.
1. 전송선 이론

[확인] 본 페이지는 exp(jωt) 시간 약속을 사용하고 있습니다.

[그림 1] 원천과 부하를 연결하는 전송선(출처: wikipedia.org)

식 (1)의 전송선 방정식(transmission line equation)으로부터 직접적으로 얻어지는 결론은 전송선 이론(transmission line theory)의 전압과 전류는 더이상 회로 이론(circuit theory)의 전압과 전류가 아님이다.

                        (1)

여기서 $R, L, G, C$는 단위길이당 해당 회로량을 의미한다. 예를 들어 $R$의 단위는 Ω/m이다. 이를 확인하기 위해 식 (1)을 $z$에 대해 미분한다.

               (2)

식 (2)는 전형적인 상수 계수(係數常數, constant coefficient) 선형 상미분 방정식(常微分方程式, linear ordinary differential equation: 하나의 독립 변수만 가진 선형적인 미분 방정식)이므로 식 (2)의 답을 아래로 가정하고 식 (2)에 대입한다.

                        (3)

그러면 미지수인 $\gamma$를 결정할 수 있다.

                        (4)

식 (4)를 식 (3)에 대입해보면 식 (2)를 만족하는 해는 두 개임을 알 수 있다. 따라서, 전송선에 발생하는 전체 전압과 전류는 아래로 표현할 수 있다.

                        (5)

여기서 $V(z)$, $I(z)$는 회로 이론에서 배운 우리가 잘 아는 전압과 전류이며, 복소수인 $V_0^+$, $V_0^-$, $I_0^+$, $I_0^-$는 전송선 이론에 새로 도입된 파동의 진폭을 나타내는 계수로서 전압과 전류에 대한 경계 조건(境界條件, boundary condition)을 이용하여 정하게 된다.[더 쉽게 현재 전송선의 초기값이나 입력이다.] 식 (5)의 $V_0^+$, $V_0^-$, $I_0^+$, $I_0^-$에 있는 ($+$)와 ($-$)는 파동의 진행 방향이다. 즉,  ($+$)는 $+z$축, ($-$)는 $-z$축으로 진행하는 파동을 뜻한다. 따라서, $V_0^+$와 $I_0^+$는 $+z$축, $V_0^-$와 $I_0^-$는 $-z$축으로 진행하는 전압파와 전류파의 크기와 $z$ = $0$에서의 기준 위상을 표현한다. 또한, 식 (5)는 페이저(phasor)를 이용하여 시간 변동을 없앤 결과이기 때문에 실제로는 공간과 시간에 대해 전송선의 전압과 전류가 변하게 된다. 공간과 시간에 대해 식 (6)과 같이 변하면 파동(波動, wave)이라 하므로 전송선의 전압과 전류는 반드시 전압파(voltage wave)와 전류파(current wave)로 생각해야 한다.

                        (6)

전압파와 전류파는 회로 이론과 전송선 이론을 구별하는 매우 중요한 개념이다. 식 (5)와 (6)에서 $I_0^-$의 앞 부호는 ($-$)로 선택한다.[부호를 ($+$)로 택해도 전혀 문제없다.] 반사 전류파는 입사 전류파와 흐르는 방향이 다르다고 가정하면 편하므로 이렇게 정한다.

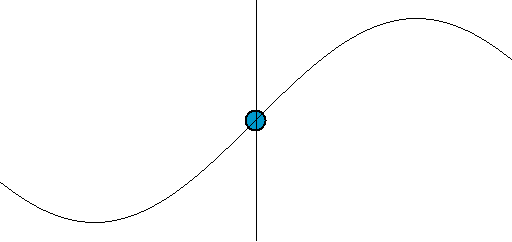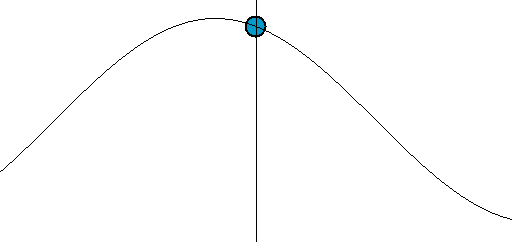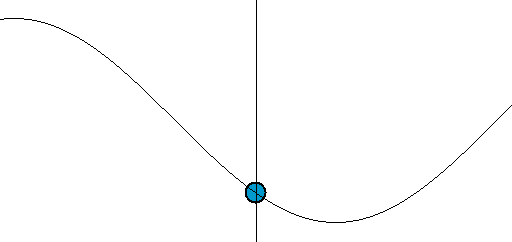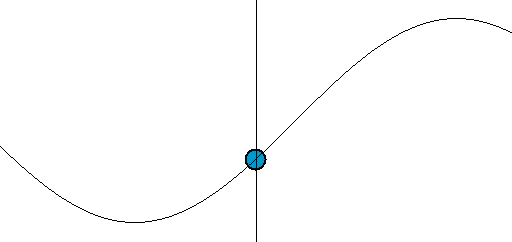
[그림 2] 전압파와 전류파의 움직임(출처: wikipedia.org)

[그림 3] 파면의 개념(출처: wikipedia.org)

[그림 2]처럼 전압파와 전류파는 전송선의 위치와 주어진 시간에 따라 계속 변하기 때문에 회로 이론처럼 어느 지점의 전압과 전류를 측정하기는 의미가 없다.[∵ 해당 위치에서 계속 변하기 때문이다.] 그래서, 전압파와 전류파가 이송하는 평균 전력(平均電力, average power)이 전송선 이론의 중요 지표이다.[평균 전력을 알려면 반사 계수(reflection coefficient)를 계산해야 한다.] 식 (6)을 잘 관찰하면 회로 이론과 전송선 이론의 차이점을 발견할 수 있다. 식 (6)의 좌변은 AC 회로 이론에서 측정하는 양이다.[∵ 전송선 방정식은 회로 이론을 기반으로 유도하기 때문에 $V(z), I(z)$는 회로 이론 양이다.] 식 (6)의 우변은 서로 반대 방향으로 진행하는 전압파와 전류파의 합성이다. 즉, 회로 이론의 전압과 전류를 파동의 성질을 가진 전압파와 전류파의 합성으로 설명할 수 있다. 예를 들면 식 (5)의 $V(z)$, $I(z)$가 회로 이론에서 정의한 전압과 전류이다. 이 전압과 전류는 전송선 이론의 입사[$V_0^+$ 항] 및 반사[$V_0^-$ 항] 전압파, 입사[$I_0^+$ 항] 및 반사[$I_0^-$ 항] 전류파로 분해해서 더 구체적으로 생각할 수 있다.

식 (6)의 우변이 파동을 의미한다는 뜻을 이해하기 위해 복소수(complex number)인 전파 상수(傳播常數, propagation constant) $\gamma$를 실수부와 허수부로 구분한다.

                       (7)

여기서 $\alpha$는 감쇠 상수(attenuation constant), $\beta$는 위상 상수(phase constant)이다. 감쇠 상수는 파동이 진행함에 따라 진폭이 얼마나 감소하는지를 나타내며 위상 상수는 파동의 진행에 따른 위상의 변동을 나타내는 상수이다. 위상 상수를 이용해 새로운 용어인 관내 파장(管內波長, guided wavelength) $\lambda_g$을 정의한다.

                       (8)

관내 파장은 전송선 내부에 존재하는 등가적인 파장(equivalent wavelength)을 뜻한다. 관내 파장은 전송선 매질과 기학 구조에 의해 결정된다.[더 정확하게 하려면 전송선의 모드(mode)까지 고려해야 한다.] 그래서 파동 방정식에 등장하는 파수(波數, wavenumber)를 위상 상수로, 파장을 관내 파장으로 비유해서 생각할 수 있다. 식 (7)을 식 (6)에 대입해서 위상만 고려하면 파동의 진행 방향도 얻을 수 있다.

                       (9)

                       (10)

파동의 움직임을 이해하려면 [그림 3]에 있는 파면(波面, wavefront)을 봐야 한다. [그림 3]을 보면 직관적으로 파동이 움직임을 느낄 수 있다. 파동이 왼쪽에서 오른쪽으로 움직이는 변화를 어떻게 인지할 수 있을까? 왜냐하면 우리가 눈으로 파면[예를 들면 꼭대기나 골짜기 등]을 추적해서 움직임을 이해하기 때문이다. 마찬가지로 식 (9)와 (10)에서 기준 파면을 $\phi_0$ = $0^\circ$인 지점으로 간주하면 이해가 된다. 시간이 $\Delta t$만큼 흐르면 식 (9)에 $\Delta z$가 $+z$ 방향으로 움직이고 식 (10)에서는 $\Delta z$가 $-z$방향으로[즉, 식 (9)와는 반대 방향으로] 움직인다. 이렇게 되는 이유는 위상 상수의 부호가 다르기 때문이다. 즉, 위상 상수가 ($+$)이면 파동은 $-z$방향으로 움직이며 위상 상수가 ($-$)이면 파동은 $+z$방향으로 움직인다. 따라서, 식 (6)의 $V_0^+, I_0^+$는 $+z$방향으로 움직이는 전압파와 전류파의 진폭이며 $V_0^-, I_0^-$는 $-z$방향으로 움직이는 전압파와 전류파의 진폭이다. 또한, 식 (9)처럼 주파수와 관내 파장의 곱이 전압파와 전류파가 움직이는 속도가 된다. 이 속도는 매질 특성인 $R, L, G, C$와 주파수에만 관계되는 상수이다. 식 (5)의 둘째식을 보면 $I_0^-$의 부호를 ($-$)로 설정한다. 이런 변화는 좀 이상하다. 이렇게 하는 이유는 전류의 방향을 바꾸기 위해서이다.[∵ 전류의 위상을 180˚ 바꾸면 전류 방향이 바뀐다.] 식 (5)와 같이 정의하면 파동의 진행 방향과 전류의 방향을 동일하게 만들 수 있어 계산할 때 매우 편해진다.[예를 들어 $I_0^-$의 부호를 ($+$)로 하면 파동은 $-z$쪽으로 움직이지만, 전류의 기준 방향은 $+z$방향이 되어 매우 불편해진다. 그래서, $I_0^-$의 부호를 ($-$)로 바꾸면 전류가 ($+$)인 방향은 $-z$쪽이 되어 계산이 편해진다.]

이상의 논의를 바탕으로 우리는 회로를 해석할 때 경우에 따라 회로 이론이나 전송선 이론을 사용할 수 있다. 언제 회로 이론을 쓰고 언제 전송선 이론을 써야 하나? 물론 전송선 이론이 정확하기 때문에 모든 회로 해석에 쓰일 수 있지만 너무 복잡하다. 회로 이론을 쓸 수 있는 곳에는 회로 이론을 쓰면 된다. 경험적으로 전송선 이론을 써야 하는 기준은 시스템의 크기 $D$가 관내 파장의 1/100보다 커지는 $D > \lambda_g / 100$ 경우이다. 예를 들어, 전송선의 길이를 1/100 파장으로 놓고, 회로 이론과 전송선 이론 간에 발생하는 위상 차이를 계산한다. 회로 이론에서는 단락된 도선을 따라 움직여도 신호의 위상은 변화가 없기 때문에, 위상차는 0˚라 생각한다. 반면 전송선에서는 전압파와 전류파의 이동으로 인해 필연적으로 위상 변화가 다음처럼 생긴다.

                       (11)

겨우 3.6˚라고 할 수도 있지만 판단 기준이 필요하기 때문에, 회로 이론을 쓸 수 있는 시스템의 크기 한계는 관내 파장의 1/100이라 생각한다. 시스템이 관내 파장보다 매우 작으면 아래 근사가 성립한다.

                       (12)

식 (12)의 우변 근사식은 많이 보던 모양이다. 이 식은 AC 회로 이론에서 사용한 페이저(phasor)이다. 사용하는 주파수가 매우 낮거나[혹은 사용하는 파장이 매우 길거나] 시스템의 크기가 매우 작으면 페이저[혹은 AC 회로 이론]만 쓰더라도 전압과 전류를 잘 예측할 수 있다. 거꾸로 주파수가 매우 높아지거나 시스템의 크기가 커진다면 회로 해석에 반드시 전송선 이론을 써야 한다.

식 (4)에서 $R$ = $G$ = $0$이 되면, 손실 없는 전송선(lossless transmission line)의 전파 상수가 된다.

                       (13)

손실을 일으키는 $R, G$가 없기 때문에 감쇠 상수가 0이 되어 손실이 없음은 당연하다. 이 경우 파동의 속도 $v$는 주파수에 관계없이 $L, C$에만 관계되어 항상 일정하게 된다.

                       (14)

식 (14)를 유전율(permittivity)과 투자율(permeability)로 표현하기 위해 커패시터(capacitor)와 인덕터(inductor)의 정의를 도입한다.

                       (15)

                       (16)

여기서 $L_{\rm ckt}, C_{\rm ckt}$는 회로 이론의 인덕턴스(inductance)와 전기 용량(capacitance)이다. 다음으로 전송선 내부에 존재하는 전자기파(electromagnetic wave)는 TEM(횡전자기, Transverse ElectroMagnetic: 진행 방향으로 전기장과 자기장 성분이 없음)파라 가정한다. TEM파는 전기장과 자기장이 서로 수직이며 전기장과 자기장의 비율[파동 임피던스: wave impedance]이 항상 일정하다. 그래서, 식 (15)와 (16)을 표현하는 좌표계를 간단하게 $(t_e, t_h, z)$로 정한다. 여기서 $t_e$는 전기장 방향 좌표이며 $t_h$는 자기장 방향 좌표이다.

                       (17)

그러므로, 전송선에 존재하는 파동의 속도는 항상 아래 식을 만족한다.

                       (18)

식 (18)은 전송선 내부에 전압파와 전류파가 존재하지만 손실이 없는 경우 그 파동의 속도는 전자기파의 속도(velocity of electromagnetic wave)와 동일함을 의미한다. 실제 전송선은 항상 손실을 가지기 때문에 $R$ = $G$ = $0$이라는 가정은 현실적이지 않다. 그래서 저손실 전송선(low loss transmission line) 개념을 도입한다. 손실이 낮으면 $R, L, G, C$ 관점에서 $R \ll \omega L$, $G \ll \omega C$라 가정한다. 그러면 식 (4)는 아래처럼 간략화된다.

                       (19)

식 (19) 유도를 위해 거듭제곱 함수(square root function)의 테일러 급수(Taylor series)를 이용한다. 재미있게도 식 (19)의 위상 상수는 손실 없는 전송선의 위상 상수인 식 (13)과 동일하다. 또한 실제 전송선로는 대부분 저손실 조건을 만족하기 때문에,[∵ 손실이 많으면 제품으로 판매할 수 없다.] 손실이 조금 있더라도 위상 상수 측면에서는 손실 없는 전송선으로 식 (19)처럼 근사가 가능하다. 그래서 실무에서는 식 (13)을 이용해 위상 상수를 근사적으로 정의한다. 식 (19)에 나타난 감쇠 상수 다음과 같이 특성 임피던스(characteristic impedance) $Z_0$를 이용해 더 간략히 표현할 수 있다.

                       (20)

여기서 $Z_0$ = $\sqrt{L/C}$ = $V_0^+/I_0^+$ = $V_0^-/I_0^-$이다. 식 (20)에 의해 $R$이 $G$보다 우세한 전송선로에서는 $Z_0$를 크게 설계해서 신호의 감쇠를 줄인다. 이는 전압파와 전류파의 특성에 기인하는 자연스러운 현상이다. 전송선로에 전류가 직렬로 흐를 때 생기는 손실 전력은 $R I^2$에 비례한다. 즉, 전류가 직렬로 흘러서 생기는 손실은 전류 자체를 줄여야 작아진다. 따라서 $Z_0$를 키우면 전압파 대비해서 전류파가 작아지기 때문에 전송선로에 생기는 전류가 줄어들어서 손실 전력이 작아진다. 이러한 전류파와 손실 전력의 관계를 식 (20)이 잘 설명하고 있다. 저항 밀도 $R$이 큰 경우와 비슷하게 컨덕턴스 밀도 $G$가 우세한 전송선로의 손실을 감소시키려면 $Z_0$를 줄여야 한다. 왜냐하면 전송선로에 병렬로 전압이 걸려서 생기는 손실은 $G V^2$에 비례하므로 $V$를 줄여야 감쇠가 줄기 때문이다. 그래서 $Z_0$를 줄이면 전류파 대비 전압파가 감소해서 $G$에 의한 손실도 적어진다.

[다음 읽을거리]
1. 특성 임피던스의 이해
2. 전압파의 반사 계수
3. 반사 전력과 투과 전력