1. 열 방정식


[그림 1] 푸리에 급수를 이용한 톱니파의 표현(출처: wikipedia.org)
통신 이론(communication theory)을 공부한 사람이면 누구나 아는 개념이 아래의 기함수(奇函數, odd function)에 대한 푸리에 급수(Fourier series)이다. 간단하게 푸리에 사인 급수(Fourier sine series)라고도 한다.
 (1)
(1)
여기서 $f(t)$는 기함수라 가정했고, $T$는 신호의 주기(period), $F_m$은 푸리에 계수(Fourier coefficient)이다. 푸리에 급수는 임의의 주기 함수(periodic function)를 삼각 함수(trigonometric function)의 무한 급수(infinite series)로 표현할 수 있어서 매우 신기하다. 경이로운 푸리에 급수를 이용해서 일반 함수의 특성을 기저 함수의 무한 급수로 분석하는 방법은 푸리에 해석(Fourier analysis)이라고 부른다. 식 (1)이 성립하기 때문에, 푸리에 계수 $F_m$은 다음과 같은 적분을 통해 쉽게 구할 수 있다.
 (2)
(2)
여기서 $F_{-m}$ = $-F_m$, 첫째식은 어떤 함수 $(\cdot)$를 한 주기 $T$에 대해 적분(integration)이다. 기함수를 한 주기에 대해 적분하면 둘째식에 있는 사인 함수(sine function)의 직교성(orthogonality: 서로 다른 두 함수를 곱해 적분하면 항상 0이 되는 성질)에 의해 셋째식이 얻어진다. 유명한 식 (2)는 푸리에Joseph Fourier(1768–1830)가 제안한 푸리에 계수를 결정하는 방법이다. 만약 $f(t)$가 우함수이면 식 (2)의 마지막 적분식에 의해 $F_m$ = $0$이 된다. 즉, 식 (2)의 적분식은 우함수와는 관계없는 식이다. 혹은 식 (2)의 적분식은 어떤 함수의 기함수 특성을 뽑는 식이라 생각할 수도 있다.[∵ 우함수 특성은 0이 되기 때문에]
여기까지는 왠만한 통신 이론 책에 나오는 내용이라 특별한 부분은 없다. 하지만 푸리에 급수를 식 (2)에 있는 적분으로 외우고 푸리에 급수의 모든 면을 다 안다고 생각하면 큰 오산이다. 푸리에 급수의 핵심은 식 (2)가 아니고 식 (1)이기 때문이다. 식 (1)이 성립하면 식 (2)는 자동적으로 얻어진다. 통신 이론을 배운 대부분의 학생들은 식 (1)을 고민하지 않는다. 식 (1)을 푸리에 급수의 정의라 생각하고 교수가 하는 말을 그대로 받아들이는 경우가 99.9%이다. 하지만 이런 학생들은 현재를 넘어서는 새로운 통신 방식을 제안할 수 없다. 식 (1)의 의미를 심각하게 고민하고 교수말을 믿지 않는 고집스러운 0.1%의 학생들이 장래에 진정한 통신공학자가 될 것이다. 푸리에 급수를 고민하지 않고는 CDMA(Code Division Multiple Access), OFDM(Orthogonal Frequency-Division Multiplexing), MIMO(Multiple-Input and Multiple-Output)와 같은 창의적인 통신 방식을 제안할 수 없다. 통신에서 푸리에 급수를 사용하는 이유는 무엇일까? 바로 신호 처리가 쉽기 때문이다. 식 (1)로 다시 돌아가 상상한다. 주기 함수 $f(t)$를 그대로 사용하기가 쉬운가 아니면 삼각 함수의 무한 급수를 사용하기가 쉬운가? 언뜻 보면 무한 급수가 없는 $f(t)$를 쓰기가 쉬울 것 같지만 우리는 주기 함수 $f(t)$에 대해 아는 부분이 없어 이 함수를 그대로 쓸 수는 없다. 하지만 푸리에 급수로 통칭하는 삼각 함수의 무한 급수는 계수 $F_m$만 결정되지 않았고 시간적 변화를 의미하는 삼각 함수는 모두 결정되어 있으므로 주기 함수 $f(t)$의 성질을 푸리에 급수를 이용해 분석할 수 있다. 따라서 시간적으로 변하는 $f(t)$를 푸리에 계수 $F_m$만으로 결정할 수 있다. 이 뜻을 제대로 이해하기가 통신 공부의 시작이다.
식 (1)은 증명이 필요한 공식이다. 푸리에가 이 방법론을 제안했을 때 가장 많은 비판을 받은 부분이 식 (1)이다. 식 (1)은 절대 정의가 아니다. 식 (1)이 푸리에 급수의 정의라면 이후 전개되는 식 (2)와 같은 내용은 동어반복이 되어 수학 이론에 심각한 결함이 된다. 대부분의 경우 식 (1)은 맞지만 모든 경우에 대해 성립하지는 않는다. 이 개념을 이해하기 위해 [그림 1]을 본다. 삼각 함수를 계속 더해가면 [그림 1]처럼 톱니파(sawtooth wave)를 근사화할 수 있다. 무한개의 삼각 함수를 더하면 톱니파를 완벽히 표현할 수 있다. 그런데 문제점이 하나 있다. $t$ = $\pm \pi, \pm 3 \pi$ 등에서 톱니파는 불연속이어서 함수값을 특정할 수 없다. 그런데 푸리에 급수는 불연속점인 $t$ = $\pm \pi, \pm 3 \pi$ 등에서 함수값이 0이라고 하고 있다. 그래서, 불연속 함수(discontinuous function) 측면으로 보면 푸리에 급수는 식 (1)을 항상 만족하지는 않는다. 따라서, 식 (1)의 등호(=)를 새롭게 바꾸어서 불연속 함수에도 적용가능하도록 해야한다.[∵ 불연속인 경우는 등호가 성립하지 않기 때문에 식 (1)을 다르게 써야 한다.] 식 (1)의 증명을 위해 푸리에 급수를 확장한다. 기함수와 전혀 다른 특성을 갖는 우함수(偶函數, even function)에 대해 푸리에 급수를 정의하면 다음과 같다. 우함수에 대한 푸리에 급수는 푸리에 코사인 급수(Fourier cosine series)라고 한다.
 (3)
(3)
식 (2)와 동일한 방법을 식 (3)에 적용하면 계수 $G_m$을 다음처럼 얻을 수 있다.
 (4a)
(4a)
여기서 $G_{-m}$ = $G_m$이다. 노이만 수(Neumann number) $\varepsilon_m$을 이용해 식 (4)에 등장한 적분을 더 편하게 표현할 수 있다.
 (4b)
(4b)여기서 $\varepsilon_m$ = $2 - \delta_{m0}$, $\delta_{ml}$은 크로네커 델타(Kronecker delta)이다. 따라서 푸리에 급수는 기함수, 우함수 여부에 따라 사인(sine) 혹은 코사인(cosine) 함수로 표현할 수 있다. 만약 $g(t)$가 기함수이면 식 (4)의 마지막 적분식에 의해 $G_m$ = $0$이 된다. 즉, 식 (4)의 적분식은 기함수와는 관계없는 식이다. 다른 측면으로 보면 식 (4)의 적분식은 어떤 함수의 우함수 특성을 추출한다.[∵ 기함수 특성은 0이 되기 때문에] 또한, 다음처럼 모든 함수는 우함수와 기함수의 합으로 표현할 수 있다.
 (5)
(5)
따라서, 식 (1)과 (3)을 합치면 우함수와 기함수 특성이 모두 합쳐지기 때문에 임의의 주기 함수에 대한 복소 푸리에 급수(complex Fourier series)를 얻을 수 있다. 복소 푸리에 급수는 기함수 혹은 우함수 여부에 관계없이 모든 주기 함수에 적용할 수 있는 일반적인 기법이다.
 (6)
(6)
식 (6)을 정리하면 다음과 같다.
 (7)
(7)
여기서 $F_{-m}$ = $-F_m$, $G_{-m}$ = $G_m$이다. 식 (2)와 (4)를 일반 함수 $h(t)$에 적용하기 위해 식 (5)처럼 $h(t)$ = $h_{\rm even}(t) + h_{\rm odd}(t)$라 한다. 다음으로 식 (2)와 (4)의 최종 결과인 $F_m$, $G_m$ 표현식을 식 (7)에 대입하면 복소 푸리에 계수 $H_m$은 다음으로 결정된다.

 (8)
(8)
혹은 식 (7)의 최종 결과인 $h(t)$ = $\sum_{m=-\infty}^\infty H_m e^{i m \omega_0 t}$를 $-T/2$에서 $T/2$까지 직접 적분해서[혹은 복소 지수 함수의 직교성을 이용해서] 식 (8)을 구할 수 있다. 푸리에 급수 개념을 정리하기 위해 복소 푸리에 급수와 푸리에 사인 및 코사인 급수의 관계를 증명한 식 (5)에서 (8)까지를 다시 본다. 우함수와 기함수 특성을 차례로 합치면 일반식인 복소 푸리에 급수가 식 (7)과 (8)처럼 얻어진다. 거꾸로 복소 푸리에 급수로부터 푸리에 사인 및 코사인 급수를 유도하려면 복소 지수 함수(complex exponential function)를 오일러 공식(Euler's formula)을 이용해 코사인과 사인으로 분해하여 식 (8)처럼 적분한다. 그러면 복소 푸리에 급수의 계수 $H_m$이 $F_m$과 $G_m$으로 나누어짐을 보일 수 있다. 푸리에 계수의 수렴 특성을 알기 위해 다음 적분식을 생각한다[1].
 (9)
(9) (10)
(10)
만약 $f(t)$가 제곱 적분 가능한 함수(square-integrable function)이면 식 (10)의 좌변이 유계(bounded)가 된다. 또한 정수 $M$은 한없이 커질 수 있으므로 식 (10)의 좌변이 무한 급수가 되더라도 유계가 된다. 따라서, $f(t)$가 제곱해서 적분 가능한 경우 푸리에 계수 제곱값의 무한 급수는 항상 수렴한다.
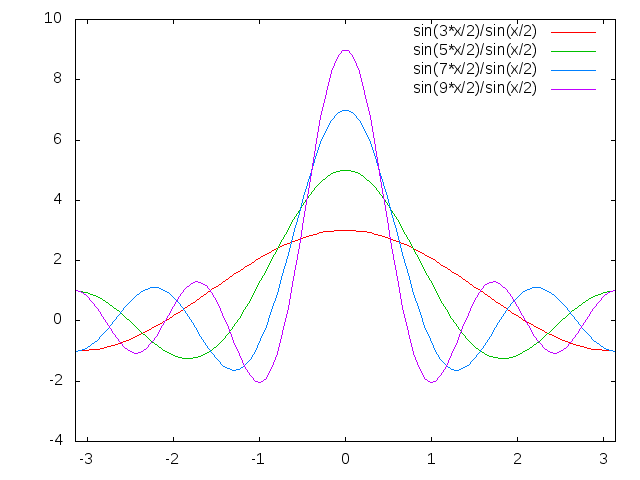
[그림 2] 디리클레 핵심의 함수값(출처: wikipedia.org)
푸리에 급수가 원래 함수로 수렴한다는 증명은 다음의 등비 급수(geometric series)부터 시작한다.
 (11)
(11)
식 (11)의 우변에 있는 등비 급수(geometric series)는 매우 중요하기 때문에 특별한 이름이 붙어있다. 푸리에 급수가 가진 원래 함수로의 수렴성을 증명한 디리클레Peter Gustav Lejeune Dirichlet(1805–1859)의 이름을 따서 다음 등비 급수를 디리클레 핵심(Dirichlet kernel)이라 부른다.
 (12)
(12)
디리클레 핵심은 등비 급수를 이용해 다음처럼 쉽게 계산할 수 있다.
 (13)
(13)
식 (12)의 디리클레 핵심을 이용해 식 (11)의 부분합 $S_M$을 다시 정의하면 다음과 같다.
 (14)
(14)
아래에서 푸리에 급수의 원래 함수 수렴성을 편하게 증명하기 위해 주기 $T$ = $2 \pi$로 가정한다. 이렇게 하더라도 일반성이 떨어지지 않는다.
[연속 함수와 푸리에 급수]
함수 $f(t)$가 연속이면 $f(t)$에 대해 다음 푸리에 급수 관계가 반드시 성립한다.
 (15)
(15)[증명: 디리클레 방법] [4]
디리클레 핵심을 한 주기에 대해 적분하면 다음을 얻을 수 있다.
 (16)
(16)여기서 $u$ = $-t'$이다. 식 (9)처럼 함수 $f(t)$와 부분합 $S_M$을 서로 빼본다. 이때 부분합은 식 (14)처럼 정의하고 함수 $f(t)$도 적분으로 바꾸기 위해 식 (16)의 둘째식을 사용한다[1]. 그러면 함수 $f(t)$와 부분합 $S_M$의 차이는 다음처럼 함수 $f(t)$를 부분합 $S_M$으로 근사한 경우의 오차값이 된다.
 (17)
(17)
다음으로 $M$을 무한대로 보내서 식 (17)의 결과가 0이 되면 증명은 끝이 난다. 하지만 이렇게 하기 전에 식 (17)에 나타난 함수 $f(t)$로 이루어진 식을 $g(t)$로 정의해서 그 특성을 좀더 세밀하게 파악한다. $f(t)$가 연속이기 때문에 $t \ne t'$인 경우는 $g(t)$도 연속이다. $t$ = $t'$이면 로피탈의 정리(L'Hôpital's rule)를 통해 다음을 얻는다.
 (18)
(18)
함수 $f(t)$가 연속이면 그 미분은 유한하므로 식 (18)의 값은 존재하며 유한하다.[∵ $0 < |t-t'| < \delta \Rightarrow |[f(t) - f(t')]/\epsilon| < 1$, 여기서 $f(t)$는 유한한 점에서만 미분 불가능일 수 있으며, $\epsilon$이 매우 작은 경우 $\delta, \epsilon$은 일대일 대응이 성립한다. 이 부분이 헷갈리면 테일러 급수(Taylor series)를 봐라.] 그래서, $g(t)$는 모든 점에서 유한하다. 이 결과를 이용해 $M$을 무한대로 보내면 다음이 성립해서 식 (15)가 증명된다.
 (19)
(19)
함수 $g(t)$가 유한한 경우 식 (19)가 성립하는 이유는 [그림 3]의 사인 함수 진동으로 설명할 수 있다.

[그림 3] 진동하는 함수의 특성(출처: wikipedia.org)
$M$이 커짐에 따라 식 (19)의 사인 함수가 빠르게 진동하므로 느리게 변하는 함수 $g(t)$가 한 번은 더해지고 한 번은 빼지므로 이를 모두 모으면[혹은 적분하면] 0으로 수렴하게 된다.
______________________________
위 증명에서 함수가 연속이면 유한한 점을 제외하고 그 미분은 유한하다는 명제를 사용한다. 이 명제는 모든 경우에 대해 참일까? 아니다. 이 부분을 규명한 바이어슈트라스Karl Weierstrass(1815–1897)의 증명으로 연속성과 미분 가능성에 대한 이해가 깊어졌다. 바이어슈트라스는 삼각 함수 급수를 이용해서 모든 점에서 연속이지만 미분의 발산으로 인해 모든 점에서 미분 불가능한 함수[2]인 바이어슈트라스 함수(Weierstrass function)를 제안했다. 연속이지만 모든 영역에서 미분 불가능한 바이어슈트라스 함수는 현실과 동떨어져 있다고 생각할 수도 있다. 하지만 바이어슈트라스 함수의 대표적인 예가 프랙탈(fractal)임을 고려하면, 연속인 미분 불가능 함수(continuous non-differentiable function)는 현실에서도 중요한 의미가 있을 수 있다. 그래서 연속이지만 프랙탈과 같은 성질을 갖는 함수는 제외해야 하므로, 위와 같은 방식으로 증명할 때는 매우 조심스럽게 접근해야 한다.
[증명: 스튀름–리우빌 이론(Sturm–Liouville theory)]
스튀름–리우빌 이론을 이용하면 쉽게 식 (15)를 증명할 수 있다. 먼저 푸리에 급수가 식 (20)에 있는 스튀름–리우빌 미분 방정식(Sturm–Liouville differential equation)을 만족함을 보인다.
 (20)
(20)다음 단계로 $p(x)$ = $1$, $q(x)$ = $0$, $r(x)$ = $1$, $\lambda$ = $m^2$을 식 (20)에 대입한다.
 (21)
(21)
즉, 복소 지수 함수는 스튀름–리우빌 미분 방정식을 만족하며 경계 조건이 주기적이므로 경계 조건이 고정되었다. 따라서, 복소 지수 함수는 고유 함수의 완비성(completeness of eigenfunctions)을 만족하여 모든 함수를 식 (15)처럼 표현할 수 있다.
______________________________
식 (19) 증명은 [그림 3]을 이용해서 대충하면 되지만 이런 정도 설명에 만족하면 진전은 별로 없다. 우리가 헷갈리는 개념은 수학의 대가들도 헷갈린다. 우리가 수양이 부족하다기보다 그 헷갈림 속에 명확하게 설명되지 아니한 수학적 진리가 있기 때문이다. 식 (19)를 명확히 증명하려면 리만–르베그 보조 정리Riemann–-Lebesgue lemma)를 이용해야 한다. 리만–르베그 보조 정리를 증명하려면 적분법의 진정한 의미를 고민해야 된다. 푸리에 급수를 연구하던 리만Bernhard Riemann(1826–1866)이 리만 적분(Riemann integral)을 새롭게 정의하고 삼각 함수 급수의 유일성을 고민하던 칸토르Georg Cantor(1845–1918)가 집합론(set theory)을 제안했던 사실은 우연이 아니다. 수학 역사에서 보면 푸리에 급수는 새로운 신천지였다. 푸리에 급수로 인해 함수(function)의 개념, 연속성과 미분 가능성, 무한 급수, 적분법, 집합론 등이 변화되었거나 새롭게 제안되었다. 푸리에는 열 방정식(heat equation)을 풀기 위한 해법으로 푸리에 급수(Fourier series)를 제안했다[6]. 열은 물리적인 실체를 가지며 측정도 가능하기 때문에 푸리에 급수가 적절한 해법임은 분명했다. 하지만 수학적으로는 결함이 있었다. 불연속 함수를 삼각 함수의 합으로 표현할 수 있다는 관찰은 푸리에 급수의 큰 문제점이었다. 푸리에 급수는 수학자 라그랑주Joseph-Louis Lagrange(1736–1813)의 사랑하는 제자 푸리에가 제안한 획기적인 방법이었지만, 수학적으로 결함이 있는 방법을 라그랑주는 절대 인정할 수가 없었다. 19세기 초반에는 불연속 함수를 함수로 취급하지 않았기 때문에 불연속 함수를 연속 함수가 될 수 있게 하는 식 (1)은 큰 결함이라 생각했다. 요즘은 이 부분이 문제가 되지는 않는다. 불연속 함수도 정의상 함수이기 때문에 이 함수를 푸리에 급수로 표현해도 수학적으로 전혀 문제가 되지 않는다. 개념을 좀더 확장하면 [그림 1]처럼 유한한 점에서 불연속인 함수도 푸리에 급수 전개가 가능하다. 디리클레가 1829년디리클레 24세, 조선 순조 시절에 증명했던 방법[4]을 참고해서 불연속점에서의 수렴 특성을 증명한다.
[조각마다 연속인 함수와 푸리에 급수]
함수 $f(t)$가 조각마다 연속(piecewise continuous)이면 다음 푸리에 급수가 반드시 성립한다.
 (22)
(22)[증명]
조각마다 연속은 함수가 유계이면서 유한한 점에서만 불연속임을 뜻한다. 식 (14)의 적분 변수를 바꾸면[$t-t' \rightarrow t'$] 다음을 쉽게 얻을 수 있다.
 (23)
(23)
식 (23)의 첫째식과 둘째식은 $t' \leftrightarrow -t'$ 변수 치환 관계를 가진다. 식 (17)처럼 주기 함수와 부분합을 빼주면 다음과 같다.
 (24)
(24)
함수 $f(t)$로 이루어진 식을 $g(t)$로 정의해서 그 특성을 본다.
 (25)
(25)
함수 $g(t)$는 $t'$ = $0$일 때만 문제가 있으므로, 이 경우의 극한을 구한다. 변수 $t'$가 항상 0보다 크면서 0으로 접근하면 식 (25)의 첫째식을 써서 계산하면 된다.
 (26)
(26)변수 $t'$가 0보다 작으면서 0으로 접근할 때는 식 (25)의 둘째식을 쓰면 된다. 따라서, $g(t)$는 모든 점에서 유한하므로 $M$이 커짐에 따라 식 (24)는 0으로 수렴한다.
______________________________
이상의 증명을 통해 푸리에 급수를 정확히 표현하려면 식 (15)가 아닌 식 (22)를 써야한다. 또한 식 (22)에 의해 식 (9)의 베셀 부등식은 항등식이 된다. 이 항등식은 파르세발의 정리(Parseval's theorem)라고 부른다.
 (27)
(27)만약 계수 $F_m$의 제곱이 아닌 $F_m$이 절대 수렴하면, 푸리에 급수는 모든 영역에서 균등 수렴한다. 푸리에 급수의 균등 수렴성은 바이어슈트라스 $M$판정(Weierstrass $M$-test)으로 손쉽게 결정한다. 디랙 델타 함수(Dirac delta function)를 이용하면 디리클레 핵심이 만드는 무한 급수를 아름답게 정의할 수도 있다. 대신 아래 식이 성립하려면, 적분 개념에 기반을 둔 리만–르베그 보조 정리가 필수적으로 적용되어야 한다.
 (28)
(28)
여기서 첫째 줄은 식 (15)에서 증명한 내용을 디리클레 핵심으로 다시 쓴 식이며 둘째 줄은 첫째 줄의 표현을 디랙 델타 함수로 다시 표기한 식이다. 물론 푸리에 급수의 완비성(completeness of Fourier series)이 성립하기 때문에 디랙 델타 함수를 식 (8)에 바로 대입해서 계산해도 식 (28)의 둘째 줄을 얻을 수 있다. 식 (28)을 다음처럼 정리하면, 충격 열(impulse train) 혹은 디랙 빗(Dirac comb)을 복소 지수 함수의 무한 급수로 나타낼 수 있다.
 (29)
(29)
[그림 4] 여러 가지 주기 함수(출처: wikipedia.org)
푸리에 급수 개념을 이용하면, 여러 초등 함수와 무한 급수의 관계를 쉽게 증명할 수 있다. 무한 급수에 대한 증명이 쉬워지는 이유는 푸리에 급수의 완비성 때문이다.
1. 급수 표현식(series representation)
[초등 함수의 급수]
 (1.1)
(1.1)
 (1.2)
(1.2)
식 (1.1)에 있는 $x$에 $x + \pi$를 대입하면 된다.
 (1.3)
(1.3)
로그 함수 $-\log(1-x)$에 대한 테일러 급수(Taylor series)를 이용해서 식 (1.3)을 증명한다.
- 톱니파(sawtooth wave)
[그림 1, 4]에 있는 톱니파를 식 (1)을 이용해 적분하면 다음을 얻는다.
 (1.4)
(1.4)
점 $x$ = $\pm \pi$ 근방에서는 불연속이며, $x$ = $\pm \pi$에서 식 (1.4)에 있는 무한 급수의 수렴값은 0이다.
- 역톱니파(reverse sawtooth wave)
[그림 1, 4]에 있는 톱니파의 좌우를 뒤집으면 역톱니파가 된다. 식 (1.4)에서 $x$ 대신 $x-\pi$를 대입하면 다음을 얻을 수 있다.
 (1.5)
(1.5)
식 (1.5)는 식 (1.3)에 제시한 무한 급수의 허수부를 선택해서 다음처럼 초등적으로 증명할 수도 있다.
 (1.6)
(1.6)
점 $x$ = $0^+$ 근처에서는 식 (1.5)의 우변이 0보다 크므로, 식 (1.6)에서 $+\pi$를 택하면 식 (1.5)의 좌변을 얻을 수 있다.
- 절대값 $|x|$
실수 $x$의 절대값에 대한 푸리에 급수는 다음과 같다.
 (1.7)
(1.7)
[그림 5] 부호 함수의 모양(출처: wikipedia.org)
- 부호 함수(sign function) $\operatorname{sgn}(x)$
[그림 5]에 있는 부호 함수의 푸리에 급수는 식 (1.7)을 미분해서 쉽게 구할 수 있다.
 (1.8)
(1.8)
여기서 부호 함수는 $x$ = $0$에서 불연속이다.
- 2차 함수(quadratic function)
2차 함수에 대해 푸리에 급수를 적용하면 다음 무한 급수를 얻을 수 있다.
 (1.9)
(1.9)식 (1.9)를 미분해서 식 (1.5)를 다시 유도할 수도 있다. 식 (1.9)에서 $x$ = $0$을 대입하면, 유명한 바젤 문제(Basel problem)의 답을 쉽게 구할 수 있다.
 (1.10)
(1.10)- 분수 복소 지수 함수(fractional complex exponential function) [5]
 (1.11)
(1.11)[참고문헌]
[1] D. Jackson, "The convergence of Fourier series," The American Mathematical Monthly, vol. 41, pp. 67–84, Feb. 1934.
[2] J. Thim, Continuous Nowhere Differentiable Functions, Master Thesis, Luleå University of Technology, Sweden, 2003.
[3] 최인혁, "해석학하는 만화 [1]: 두 번 미분하기", HORIZON, 2019년 6월. (방문일 2019-10-01)
[3] 최인혁, "해석학하는 만화 [1]: 두 번 미분하기", HORIZON, 2019년 6월. (방문일 2019-10-01)
[4] P. G. L. Dirichlet, "Sur la convergence des séries trigonométriques qui servent à représenter une fonction arbitraire entre des limites données (On the convergence of trigonometric series which serve to represent an arbitrary function between given limits)," Journal für die reine und angewandte Mathematik (Journal for Pure and Applied Mathematics), vol. 4, pp. 157–169, 1829.
[5] M. V. Berry, "Optical vortices evolving from helicoidal integer and fractional phase steps," J. Opt. A: Pure Appl. Opt., vol. 6, no. 2, pp. 259–268, Jan. 2004.
[6] 이정오, "무한급수의 총합 가능성과 후세인 보르에 관하여", 한국수학사학회지, 제30권, 제6호, pp. 353–365, 2017년 12월.
[7] 박원우, 딥러닝을 위한 푸리에 영상처리, 홍릉, 2023.
[다음 읽을거리]
1. 푸리에 변환
2. 리만–르베그 보조 정리
























 (21)
(21)

